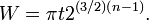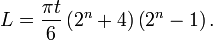Britney Gallivan

Britney Gallivan

Britney Gallivan

Britney Gallivan (de Pomona, California) es conocida principalmente por haber determinado el número máximo de veces que se puede doblar un determinado papel u otro material no comprimible.

Contenido

Biografía

En Enero de 2002, siendo todavía estudiante de secundaria, Gallivan demostró que un único trozo de papel de 4.000 pies (aproximádamente 1200m) de longitud puede ser doblado por la mitad doce veces. Hasta entonces se creía empíricamente que el límite era únicamente 8 veces. También dobló una lámina cuadrada de oro por la mitad 12 veces. No solo realizó la demostración empírica, sino que también dedujo una ecuación para calcular la anchura del papel W necesaria para doblar una hoja de grosor t un número dado de veces n.

En Mayo de 2007 Britney Gallivan se graduó por la Universidad de California, Berkeley con un diploma en Ciencia Medioambiental del Colegio de Recursos Naturales.

Teorema del doblado de papel

Para un doblado en direcciones alternas de n veces, la anchura de papel necesaria tiene un límite superior y aproximación cercana de

W = \pi t 2^{(3/2)\left(n-1\right)}.

Para dobleces en una única dirección (utilizando una tira de papel larga), la longitud exacta L de papel necesaria es

L = \frac{\pi t}{6}\left(2^{n}+4\right)\left(2^{n}-1\right).

Véase también

Enlaces externos

Obtenido de "Britney Gallivan"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Britney Gallivan — (born c. 1986) of Pomona, California is best known for determining the maximum number of times which paper or other non compressible materials can be folded. BiographyIn January 2002, while a junior in high school, Gallivan demonstrated that a… …   Wikipedia

  • Britney — La palabra Britney puede referirse a: Britney Spears, cantante estadounidense. Britney, álbum de Britney Spears. Britney Stevens, actriz estadounidense. Britney Gallivan, personaje estadounidense. Esta página de desambiguación cataloga artículos… …   Wikipedia Español

  • Mathematics of paper folding — The art of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model s flat foldability (whether the model can be flattened without damaging it) and the use of paper folds to …   Wikipedia

  • Matemáticas del origami — Se han realizado numerosos estudios matemáticos acerca del arte del plegado de papel papiroflexia u origami. Los aspectos que han despertado interés matemático incluyen la capacidad de aplastar sin dañar una determinada figura de papel (problema… …   Wikipedia Español

  • List of amateur mathematicians — This is a list of amateur mathematicians people whose primary vocation did not involve mathematics (or any similar discipline) yet made notable, and sometimes important, contributions to the field of mathematics. In general, they are not listed… …   Wikipedia

  • Paper folding — is the art of folding paper; it is known in many societies that use paper. In much of the West, the term origami is used synonymously with paper folding, though the term properly only refers to the art of paper folding in Japan.Forms of paper… …   Wikipedia

  • Ограничение складывания бумаги пополам — Ограничение складывания бумаги пополам  физический феномен, суть которого состоит в том, что лист обычной бумаги офисного размера A4 можно сложить пополам не более 7 раз. Он происходит из за быстроты роста показательной функции. Количество… …   Википедия

  • Закон складывания бумаги — Ограничение складывания бумаги пополам  явление в природе. Суть феномена состоит в том, что лист обычной бумаги офисного размера можно сложить пополам не более 7 раз. Он происходит из за быстроты роста показательной функции. Число слоёв бумаги… …   Википедия

  • List of mathematicians (G) — NOTOC Gab * Gabai, David (?, ? ) * Gage, Paul (?, ? ) * Gage, Walter (Canada, 1922 1978) * Gaitsgory, Dennis (USA, ? ) * Galambos, Janos (USA/Hungary, 1940 ) * Gale, David (USA, 1921 2008) * Galerkin, Boris Grigoryevich (Russia, 1871 1945) *… …   Wikipedia

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”