- Buscaminas
-
Buscaminas
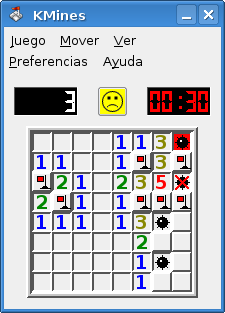Captura de pantalla de una versión del buscaminas
El Buscaminas (en inglés: Minesweeper) es un videojuego para un jugador inventado por Robert Donner en 1989. El objetivo del juego es despejar un campo de minas sin destapar ninguna mina.
El juego ha sido programado para muchos sistemas operativos, pero debe su popularidad por la versión que viene con Microsoft Windows.
Contenido
Reglas
El juego consiste en despejar todas las casillas de una pantalla que no oculten una mina.
Algunas casillas tienen un número, este número indica las minas que suman todas las casillas circundantes. Así si una casilla tiene el número 3 significa que de las ocho casillas que hay alrededor (si no está en una esquina o borde) hay 3 con minas y 5 sin minas. Si se descubre una casilla sin número indica que ninguna de las casillas vecinas tiene mina y estas se descubren automáticamente.
Si se descubre una casilla con una mina se pierde la partida.
Se puede poner una marca en las casillas que el jugador piensa que hay minas para ayudar a descubrir la que están cerca.
El juego también posee un sistema de récords para cada uno de Los 4 niveles en el que se indica el menor tiempo en terminar el juego. Los niveles son (para las nuevas versiones):
- Nivel principiante: 9 × 9 casillas y 10 minas.
- Nivel intermedio: 16 × 16 casillas y 40 minas.
- Nivel experto: 16 × 30 casillas y 99 minas.
- Nivel personalizado: en este caso el usuario personaliza su juego eligiendo el número de minas y el tamaño de la cuadricula
En versiones anteriores a Windows 2000 la pantalla en nivel principiante sólo mide 8 × 8, y fue agrandada para evitar que la probabilidad de hacer clic en una mina fuera la misma que en el nivel intermedio: 10/(8×8) = 10/64 = 40/256 = 40/(16×16)
También se puede personalizar la dificultad de juego según el tamaño de la pantalla y el número de minas.
En Windows XP el buscaminas tiene sonido. En Windows Vista se elimina la carita feliz que venía apareciendo en versiones anteriores de Windows, además agrega nuevos efectos y la posibilidad de cambiar las minas por flores.
Elementos de análisis en el juego
El juego tiene reglas muy sencillas, pero es de interés en matemáticas.
No siempre se puede resolver sin recurrir a la suerte
A veces hay que elegir de forma aleatoria por falta de información. Por ejemplo, en la siguiente situación:
(
representa una mina, y los números son los números estándar del Buscaminas.)El jugador debe adivinar cuál de los dos cuadrados marcados con un ? es una mina. Los números no dan ninguna información sobre cuál es la mina, así que el jugador tendrá que recurrir a la suerte o las probabilidades que son calculables en estos casos.
Juego NP-completo
El siguiente es un problema interesante: dado un tablero con los números, ¿será válido? En otras palabras, ¿existe alguna combinación de minas en los cuadrados ocultos que sea consistente con dichos números? Este problema se sabe que es NP-completo. Es decir, es fácil comprobar que una colocación determinada de minas corresponde a los números dados, pero es probablemente difícil dar con dicha colocación. Esto puede querer decir que a veces es difícil jugar perfectamente al Buscaminas.
Las probabilidades de descubrir una mina no son suficientes
Si por "juego perfecto" se entiende encontrar una estrategia que asegure la mejor probabilidad de resolver una partida cualquiera, entonces se requieren más cosas que limitarse a elegir los cuadrados que ofrezcan la menor probabilidad de mina. Examinemos la siguiente situación:
(Como en el ejemplo anterior,
representa una mina, y los números son los números estándar del Buscaminas; a, b, c, d y e son las posiciones desconocidas.)La probabilidad de descubrir una mina en a, b o c es de 2/3, y la de descubrir una mina en d o e es de 1/2; esto se puede comprobar computando las 6 posibilidades de colocar minas en a+b+c+d+e. Sin embargo, destapar d o e no proporciona ninguna información útil: si no se descubre una mina aparecerá un 6 en e o un 5 en d. En el juego conjunto, d o e permite ganar la partida en sólo 1 de los 6 casos posibles. Sin embargo, al destapar a, b o c, si no se descubre una mina la información permitirá saber si hay una mina en d o no, y en el juego conjunto se puede ganar la partida en 2 de los 6 casos posibles. Así que jugar a, b o c, aunque a corto plazo sea más arriesgado, acaba siendo la mejor jugada.
Variaciones
Buscaminas en 3 dimensiones
Online, non rectangular
Buscaminas hexagonal
Buscaminas triangular
Buscaminas ASCII
Buscaminas que siempre genera partidas que pueden resolverse sin necesidad de adivinar
Enlaces externos
Categorías: Videojuegos para Windows | Videojuegos de lógica | Videojuegos de 1989 | Problemas NP-completos
Wikimedia foundation. 2010.
