En informática, la búsqueda por fuerza bruta, búsqueda combinatoria, búsqueda exhaustiva o simplemente fuerza bruta, es una técnica trivial pero a menudo usada, que consiste en enumerar sistemáticamente todos los posibles candidatos para la solución de un problema, con el fin de chequear si dicho candidato satisface la solución al mismo.

Por ejemplo, un algoritmo de fuerza bruta para encontrar el divisor de un número natural n consistiría en enumerar todos los enteros desde 1 hasta n, chequeando si cada uno de ellos divide n sin generar resto. Otro ejemplo de búsqueda por fuerza bruta, en este caso para solucionar el problema de las ocho reinas (posicionar ocho reinas en el tablero de ajedrez de forma que ninguna de ellas ataque al resto), consistiría en examinar todas las combinaciones de posición para las 8 reinas (en total 64! /56! = 178.462.987.637.760 posiciones diferentes), comprobando en cada una de ellas si las reinas se atacan mutuamente.

La búsqueda por fuerza bruta es sencilla de implementar y, siempre que exista, encuentra una solución. Sin embargo, su coste de ejecución es proporcional al número de soluciones candidatas, el cual es exponencialmente proporcional al tamaño del problema. Por el contrario, la búsqueda por fuerza bruta se usa habitualmente cuando el número de soluciones candidatas no es elevado, o bien cuando éste puede reducirse previamente usando algún otro método heurístico.

Es un método utilizado también cuando es más importante una implementación sencilla que una mayor rapidez. Este puede ser el caso en aplicaciones críticas donde cualquier error en el algoritmo puede acarrear serias consecuencias, o también en aplicaciones destinadas a . Bor rute-force search is also useful as "baseline" method when benchmarking other algorithms or metaheuristics. Indeed, brute-force search can be viewed as the simplest metaheuristic.

La búsqueda por fuerza bruta no se debe confundir con backtracking, método que descarta un gran número de conjuntos de soluciones, sin enumerar explícitamente cada una de las mismas.

Contenido 1 Implementación de la búsqueda por fuerza bruta 1.1 Algoritmo básico 1.2 Variaciones comunes en el algoritmo 2 Explosión combinacional 3 Véase también

Implementación de la búsqueda por fuerza bruta

Algoritmo básico

Para poder utilizar la búsqueda por fuerza bruta a un tipo especifico de problema, se deben implementar las funciones primero, siguiente, valido, y mostrar. Todas recogerán el parámetro P indicando una instancia en particular del problema:

1. primero (P): genera la primera solución cadidata para P.
2. siguiente (P, c): genera la siguiente solución candidata para P después de una solución candidata c.
3. valido (P, c): chequea si una solución candidata c es una solución correcta de P.
4. mostrar (P, c): informa que la solución c es una solución correcta de P.

La función siguiente debe indicar de alguna forma cuándo no existen más soluciones candidatas para el problema P después de la última. Una forma de de realizar esto consiste en devolver un valor "nulo". De esta misma forma, la función primero devolverá un valor "nulo" cuando no exista ninguna solución candidata al problema P.

Usando tales funciones, la búsqueda por fuera bruta se expresa mediante el siguiente algoritmo:

c 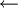 primero(P)
mientras c != null
  si valido(P,c) entonces mostrat(P, c)
  c 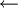 siguiente(p,c)

Por ejemplo, para buscar los divisores de un entero n, la instancia del problema P es el propio número n. la llamada primero (n) devolverá 1 siempre y cuando n 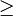1, y "nulo" en otro caso; la función siguiente (n,c) debe devolver c + 1 si c < n, y "nulo" caso contrario; valido (n,c) devolverá verdadero si y solo si c es un divisor de n.

Variaciones comunes en el algoritmo

El algoritmo descrito anteriormente llama a la función mostrar para cada solución al problema. Éste puede ser fácilmente modificado de forma que termine una vez encuentre la primera solución, o bien después de encontrar un determinado número de soluciones, después de probar con un número especifico de soluciones candidatas, o después de haber consumido una cantidad fija de tiempo de CPU.

Explosión combinacional

La principal desventaja del método de fuerza bruta es que, para la mayoría de problemas reales, el número de soluciones candidatas es prohibitivamente elevado.

Por ejemplo, para buscar los divisores de un número n tal y como se describe anteriormente, el número de soluciones candidatas a probar será de n. Por tanto, si n consta de, digamos, 16 dígitos, la búsqueda requerirá de al menos 10¹⁵ comparaciones computacionales, tarea que puede tardar varios días en un ordenador personal tipo. Si n es un bit de 64 dígitos, que aproximadamente puede tener hasta 19 dígitos decimales, la búsqueda puede tardar del orden de 10 años.

Este crecimiento exponencial en el número de candidatos, cuando crece el tamaño del problema ocurre en todo tipo de problemas. Poe ejemplo, si buscamos una combinación particular de 10 elementos entonces tendremos que considerar 10! = 3,628,800 candidatos diferentes, lo cual en un PC habitual puede ser generado y probado en menos de un segundo. Sin embargo, añadir un único elemento más — lo cual supone solo un 10% más en el tamaño del problema — multiplicará el número de candidatos 11 veces — lo que supone un 1000% de incremento. Para 20 elementos el número de candidatos diferentes es 20!, es decir, aproximadamente 2.4×10¹⁸ o 2.4 millones de millones de millones; la búsqueda podría tardar unos 10.000 años. A este fenómeno no deseado se le denomina explosión combinacional.

Véase también

• Ataque de fuerza bruta
• big O notation