Circunferencia osculatriz

Circunferencia osculatriz
Circunferencia osculatriz.

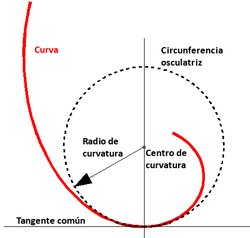
En geometría diferencial de curvas, la círcunferencia osculatriz (del latín osculari 'besar') o círculo osculador a una curva en un punto dado es una circunferencia cuyo centro se encuentra sobre la normal a la curva y tiene la misma curvatura que la curva dada en ese punto. El centro y el radio de la circunferencia osculatriz en un punto de la curva son llamados centro de curvatura y radio de curvatura de la curva en ese punto. El plano en el que está contenida la circunferecia osculatriz se denomina plano osculador.

La circunferencia osculatriz tiene con la otra curva un contacto de segundo orden en el punto considerado, o sea, las primeras y las segundas derivadas de ambas curvas son iguales.

Esta circunferencia, que es [[tangente]] en el punto dado a la curva fue llamado "circulum osculans" ("círculo que besa") por Leibniz.

Obtención

Una construcción geométrica de la circunferencia osculatriz fue descrita por Isaac Newton en su Principia:

There being given, in any places, the velocity with which a body describes a given figure, by means of forces directed to some common centre: to find that centre.
Isaac Newton, Principia; Proposition V. Problem I.

Dados tres puntos de una curva (no necesariamente plana), existe un único plano y una circunferencia contenida en este plano que contiene a los tres puntos. Si los puntos se toman suficientemente próximos entre sí, la circunferencia definida por la construcción anterior constituye una aproximación a la circunferencia osculatriz en el punto intermedio de los tres dados. Si se imagina un proceso de paso límite de tal manera que los tres puntos acaben coincidiendo, la circunferencia límite obtenida es precisamente la circunferencia osculatriz. Este proceso de límite es análogo al seguido para obtener la recta tangente a una curva haciendo coincidir dos puntos arbitrariamente cercanos.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • osculatriz — osculatriz. (Del lat. osculari, besar). adj. Geom. Dicho de una circunferencia: Que tiene con otra curva un contacto de segundo orden en el punto considerado, o sea, cuando las primeras y las segundas derivadas de ambas son iguales. U. t. c. s. f …   Enciclopedia Universal

  • osculatriz — (Del lat. osculari, besar). adj. Geom. Dicho de una circunferencia: Que tiene con otra curva un contacto de segundo orden en el punto considerado, o sea, cuando las primeras y las segundas derivadas de ambas son iguales. U. t. c. s. f.) …   Diccionario de la lengua española

  • Aceleración — En física, la aceleración es una magnitud vectorial que nos indica el cambio de velocidad por unidad de tiempo. En el contexto de la mecánica vectorial newtoniana se representa normalmente por o y su módulo por . Sus dimensiones son . Su unidad… …   Wikipedia Español

  • curvatura — ► sustantivo femenino Condición de lo que es curvo: ■ es preciso modificar la curvatura del arco. SINÓNIMO [curvidad] * * * curvatura 1 f. Cualidad de curvo. ⊚ Forma curva. 2 Acción de curvar[se]. * * * curvatura. (Del lat. curvatūra). f.… …   Enciclopedia Universal

  • curvatura — (Del lat. curvatūra). f. Cualidad de curvo; desviación continua respecto de la dirección recta. En una circunferencia es la inversa del radio; en otra curva cualquiera es la inversa del radio de la circunferencia osculatriz. ☛ V. línea de doble… …   Diccionario de la lengua española

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”