- Matemática
-
Portal:Matemática
Portal de MatemáticaPortal 
WikiProyecto
Destacados
BuenosIntroducciónLa Matemática (del griego μάθημα, máthema: ciencia, conocimiento, aprendizaje, μαθηματικóς, mathematikós: amante del conocimiento) es el estudio de patrones en las estructuras de entes abstractos y en las relaciones entre ellas. Algunos matemáticos se refieren a ella como la "Reina de las Ciencias". En español también se puede usar el término en plural: Matemáticas.
Aunque la matemática sea la supuesta "Reina de las Ciencias", ella misma no se considera una ciencia natural. Principalmente, los matemáticos definen e investigan estructuras y conceptos abstractos por razones puramente internas a la matemática, debido a que tales estructuras pueden proveer, por ejemplo, una generalización elegante, o una útil herramienta para cálculos frecuentes. Además, muchos matemáticos estudian sus áreas de preferencia simplemente por razones estéticas, viendo así la matemática como una forma del arte en vez de una ciencia práctica o aplicada. Sin embargo, las estructuras que los matemáticos investigan frecuentemente sí tienen su origen en las ciencias naturales, y muchas veces encuentran sus aplicaciones en ellas, particularmente en la Física.
Artículo
Construcción de un
pentágono regularLa construcción con regla y compás es el trazado de puntos, segmentos de recta y ángulos usando exclusivamente una regla y compás idealizados. La geometría clásica griega impuso esa norma para las construcciones, aunque los griegos también investigaron las que pueden obtenerse con instrumentos menos básicos.
Los problemas más famosos que se propusieron para su resolución con regla y compás son la cuadratura del círculo, la duplicación del cubo y la trisección del ángulo, a los que a veces se añade la construcción del heptágono regular, el primero de los infinitos polígonos regulares imposibles de crear con regla y compás. Tienen en común ser de resolución imposible: está matemáticamente demostrado que no se puede cuadrar el círculo, ni duplicar el cubo, ni trisecar el ángulo, ni trazar un heptágono regular usando exclusivamente la regla y el compás idealizados de la geometría griega.
Archivo portadaImagen destacada
Espiral de Ulam. Nótese cómo los números primos están más presentes en unas diagonales que en otras.
Cita Matemática«¡Cómo es posible que la matemática, un producto del pensamiento humano independiente de la experiencia, se adapte tan admirablemente a los objetos de la realidad!» Einstein . Físico
¿Sabías que...- La espiral de Ulam es una curiosa forma gráfica de representación de los números naturales.
- La función de Weierstrass es continua en todo punto y no es derivable o diferenciable en ninguno.
- La trompeta de Torricelli es una figura geométrica que tiene la característica de poseer una superficie infinita pero un volumen finito.
- Es fácil saber si un ente está encerrado en una curva cerrada simple utilizando el teorema de la curva de Jordan.
- El descubrimiento del cálculo es obra de Gottfried Wilhelm Leibniz e Isaac Newton.
- 0.999... = 1.
- La constante de Chaitin es definible, pero no es computable.
- Sólo hay 5 poliedros regulares convexos en 3 dimensiones. Son los llamados sólidos platónicos.
- En teoría de conjuntos, hay varias clases de infinitos, dependiendo de su cardinalidad. El cardinal del conjunto de los números naturales es
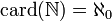(alef-0). - El ortocentro, el circuncentro y el baricentro de cualquier triángulo están contenidos en una recta llamada recta de Euler.
- El número 40337956 se puede escribir como 40-33+79-56.
- Todos los números primos de la forma p = 4k+1 pueden escribirse como suma de dos cuadrados.
ArchivoBiografía
Evariste Galois
Conocido por:
ArchivoSubdivisiones de la matemáticaGeneral
Teoría de números
Álgebra
Geometría
- Teoría de conjuntos
- Historia de la matemática
- Historia de la Geometría
- Matemáticos
- Matemática recreativa
- Lógica matemática
- Filosofía de la matemática
- Demostración matemática
- Símbolos matemáticos
- Lista de Axiomas y Teoremas
- Aritmética
- Número
- Teorema fundamental de la Aritmética
- Porcentaje
- Aritmética computacional
- Conjetura de Goldbach
- Número primo
- Triángulo de Pascal
- Pequeño teorema de Fermat
- Teorema de Wilson
- Más artículos...
- Polinomio
- Ecuación
- Álgebra abstracta
- Teoría de grupos
- Teoría de Anillos
- Cuerpo
- Dominio de integridad
- Teoría de Galois
- Álgebra conmutativa
- Álgebra lineal
- Aplicación lineal
- Espacio vectorial
- Matriz
- Álgebra multilineal
- Más artículos...
- Geometría analítica
- Geometría proyectiva
- Geometría euclidiana
- Geometría no euclidiana
- Geometría diferencial
- Sistemas dinámicos
- Grupo de Lie
- Más artículos...
Análisis matemáticoTopología
Estadística y Probabilidad
Matemática discreta
- Cálculo
- Análisis numérico
- Análisis complejo
- Análisis funcional
- Espacio prehilbertiano
- Funcional continuo
- Espacio de Hilbert
- Más artículos...
-
- Espacio topológico
- Función continua
- Fibrado
- Grupos topológicos
- Topología algebraica
- Característica de Euler
- Functor
- Grupos de homotopía
- Grupos de homología
- Homotopía
- Topología geométrica
- Más artículos...
- Matemática financiera
- Biología matemática
- Criptografía
- Teoría del Caos
- Optimización
- Más artículos...
CategoríasÁlgebra | Análisis matemático | Aritmética | Combinatoria | Ecuaciones diferenciales | Estadística | Física matemática | Funciones especiales | Geometría | Matemática aplicada | Matemática discreta | Principios y leyes matemáticas | Probabilidad | Teoremas | Teoría de la demostración | Teoría de categorías | Teoría de conjuntos | Teoría de grafos | Teoría de números | Teoría del caos | Teoría del orden | Topología | Transformaciones
Conjeturas matemáticas | Documentales de matemática | Historia de la matemática | Matemática recreativa | Matemáticos | Paradojas | Premios de matemática | Problemas matemáticos
Anexos de Matemática
.Wikimedia
WikilibrosMatemáticas LOGSE 
| Teoría de conjuntos 
| Cálculo en una variable | Álgebra Lineal 
- ... Más Wikilibros de Matemática
CommonsImágenes y Multimedia sobre matemáticas. 
Wikiversidad.Departamento de Matemática 
WikiquoteCitas de Matemática | Citas de Matemáticos Portales Relacionados
Álgebra Física Ingeniería Ciencia Informática Tecnología 
Acceder a los otros portales temáticos de la Wikipedia en Español
Categorías: Matemáticas | Wikipedia:Portales de ciencias formales
Wikimedia foundation. 2010.
