Cisoide de Diocles

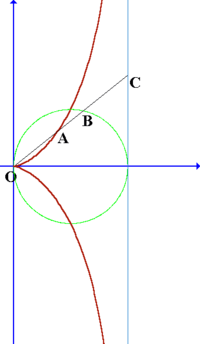
Cisoide de Diocles: Cisoide de Diocles (línea roja). El segmento OA es igual a OC menos OB.

La cisoide de Diocles es la cisoide generada por el vector posición de una recta paralela al eje OY (Curva 1), que pasa por el punto (2a,0), al que se le resta el radio vector de una circunferencia de radio a y centro en (0,a) (Curva 2).

Su ecuación, en coordenadas polares es:

$\rho=\rho_1 - \rho_2= \frac {2a}{\cos\omega} - 2a\, \cos\omega = 2a \frac {\mathrm{sen}^2\omega}{\cos\omega}$

Y en cartesianas:

$y^2=\frac {x^3}{2a-x}$

Véase también

Cisoide

Referencias

Mataix Lorda, Mariano (1986). «La duplicación del cubo. La cisoide de Diocles». Historias de matemáticos y algunos problemas. Marcombo. pp. 85-88. ISBN 8426706118.

Enlaces externos

Weisstein, Eric W. «Cisoide de Diocles» (en inglés). MathWorld. Wolfram Research.

"Cissoid of Diocles" en Visual Dictionary Of Special Plane Curves (en inglés)

"Cissoid of Diocles" at MacTutor's Famous Curves Index (en francés)

"Cissoid" en 2dcurves.com (en inglés)

"Cissoïde de Dioclès ou Cissoïde Droite" en Encyclopédie des Formes Mathématiques Remarquables (en francés)

"The Cissoid" An elementary treatise on cubic and quartic curves Alfred Barnard Basset (1901) Cambridge pp. 85ff (en inglés)

Categorías:
Curvas
Curvas algebraicas

Игры ⚽ Поможем сделать НИР

Cisoide — Ejemplo de cisoide media. Se llama cisoide a la curva generada por la suma de los vectores posición de dos curvas dadas. Sean C1 y C2 dos curvas definidas por las siguientes ecuaciones en coordenadas polares: y … Wikipedia Español
Podaria — Saltar a navegación, búsqueda Se llama podaria de la curva C con respecto al punto P al lugar geométrico de las proyecciones ortogonales de P sobre las tangentes de la curva C (Vea la figura). Dada la curva C(x,y)=0, su tangente en el punto… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico