Resistencia a la rodadura

Resistencia a la rodadura

La resistencia a la rodadura se presenta cuando un cuerpo rueda sobre una superficie, deformándose uno de ellos o ambos. Como veremos, no tiene sentido alguno hablar de resistencia a la rodadura en el caso de un sólido rígido (indeformable) que rueda sobre una superficie rígida (indeformable).

El concepto de coeficiente de rodadura es similar al de coeficiente de rozamiento, con la diferencia de que este último hace alusión a dos superficies que deslizan o resbalan una sobre otra, mientras que en el coeficiente de rodadura no existe tal resbalamiento entre la rueda y la superficie sobre la que rueda, disminuyendo por regla general la resistencia al movimiento.

Contenido

Generalidades

Por un lado, a escala microscópica una rueda no presenta un alzado exactamente circular, y la superficie sobre la que rueda no constituye tampoco un perfil plano, puesto que en ambos casos existen irregularidades. No obstante, este no es el principal factor que influye en el coeficiente, sino la histéresis. La rueda, en función del material con el que esté construida y su propio peso, además del de la carga que soporta, sufre una deformación que al rotar provoca repetidos ciclos de deformación y recuperación, estos ciclos propician la disipación de energía por calor. Además, esta deformación supone que no apoye una línea únicamente sobre el piso, sino una superficie.

El fin del coeficiente de rodadura es establecer un parámetro empírico, sobre el conjunto completo, que proporcione la fuerza que se ha de ejercer bien para poner en movimiento el sistema (coeficiente de rodadura estático), o bien para mantener su velocidad (coeficiente de rodadura dinámico). Este último también depende de la velocidad.

Desarrollo del concepto

Figura 1. Deformación en la generatriz de apoyo.
Figura 2. Rodadura de un cilindro indeformable sobre un pavimento indeformable.
Figura 3. Rodadura de un cilindro deformable sobre un pavimento indeformable.

En efecto, la resistencia a la rodadura aparece cuando el cuerpo que rueda, o la superficie sobre la que rueda, o ambos a la vez, se deforman, aunque sólo sea ligeramente, a causa de las grandes presiones existentes en los puntos de contacto. Pensemos en el caso de un cilindro que se apoya sobre una superficie plana; todo el peso del cilindro gravita sobre una exigua superficie de contacto (una generatriz, desde un punto de vista estrictamente geométrico). Es fácil comprender que la presión en el contacto será tan grande que hasta el material más rígido se deformará. De ese modo, el cuerpo, la superficie que lo soporta o ambos, se deforman, aumentando el área de contacto hasta que la presión disminuye y se restablece una situación de equilibrio elastostático. En resumen, al rodar un cuerpo real sobre una superficie real se producen unas deformaciones, como se muestra en la Figura 1, de modo que el cuerpo tiene que "vencer" continuamente un pequeño obstáculo que se le presenta por delante y que se opone a su rodadura.

Cuerpos rígidos (ideales)

Consideremos, para comenzar, el caso ideal de un cuerpo indeformable (un cilindro o una rueda, por ejemplo) que puede rodar sobre una superficie plana también indeformable (Figura 2). Si la superficie es horizontal, las fuerzas que actúan sobre el cilindro son: su peso P\, y la reacción normal del plano N\, . Si ahora aplicamos una fuerza F\, sobre el eje del cilindro, paralelamente al plano y perpendicularmente al eje, aparecerá una fuerza de rozamiento, f\, , en A, en dirección opuesta a la fuerza aplicada F\, . El momento de la fuerza de rozamiento respecto del eje del cilindro, M=fR\, hace girar el cilindro alrededor de su eje. Así, en el caso de cuerpos indeformables soportados por superficies indeformables, por pequeña que sea la fuerza F\, se producirá la rodadura (siempre que exista suficiente rozamiento estático para evitar el deslizamiento). En estas condiciones no tienen sentido hablar de resistencia a la rodadura.

Cuerpos deformables (reales)

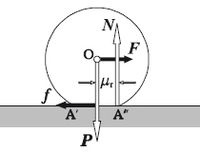
En las situaciones reales, los cuerpos se deforman, por poco que sea. El contacto no se realiza entonces a lo largo de una generatriz (como en el ejemplo anterior) sino a lo largo de una estrecha banda A′A″, como se muestra en la Figura 3. Ello da lugar a que aparezcan reacciones en los apoyos; reacciones que dan lugar a la aparición de un par que se opone la rodadura. Con la finalidad de simplificar el problema, podemos imaginar que en cada instante el cilindro debe rotar sobre la generatriz que pasa por A″ para poder rodar superando el pequeño obstáculo que se opone a ello. Eso equivale a considerar desplazada la línea de acción de la reacción normal N una distancia que designaremos por μr, como se muestra en la Figura 3. El par de resistencia a la rodadura y el par aplicado valen, respectivamente

(1) M_\text{res}=\mu_\text{r} N\,

(2) M_\text{apl}=RF\,

En las condiciones críticas, cuando comienza la rodadura, esos el par aplicado o de aranque será mayor que el par resistente, de modo que

(3) M_\text{arranque} \ge M_\text{apl} \qquad\Rightarrow\qquad RF \ge \mu_\text{r} N\,

de modo que el cilindro comenzará a rodar si

(4) F \ge \frac{\mu_{\text{r}}N}{R}=C_\text{rr} N

que nos da el valor de la fuerza mínima necesaria para el arranque.

Coeficientes

La magnitud \mu_{\text{r}}\,, que tiene dimensiones de una longitud, es el llamado coeficiente de resistencia a la rodadura. De las expresiones anteriores se deduce que el par de arranque es proporcional a la reacción normal N\, y que la fuerza de tracción necesaria para el arranque es inversamente proporcional al radio del cilindro; esa es la ventaja de las ruedas grandes sobre las pequeñas. El valor del coeficiente \mu_{\text{r}}\, depende de la naturaleza de los cuerpos en contacto (fundamentalmente de su rigidez).

La magnitud adimensional

(5) C_\text{rr}=\frac{\mu_{\text{r}}}{R}

es el llamado coeficiente de rodadura.

En general, el coeficiente de rodadura tiene un valor muy inferior al de los coeficientes de rozamiento por deslizamiento (estático y cinético); así pues, es mucho más conveniente, al efecto de disminuir las pérdidas energéticas, sustituir en los mecanismos y máquinas los deslizamientos por las rodaduras; esa es la ventaja que aportó el invento de la rueda, la ventaja del carro sobre el trineo.

La dependencia del coeficiente de rodadura con el peso del sistema, a diferencia del coeficiente de rozamiento, hace que no sea siempre operativo calcular el coeficiente de rodadura a través del ángulo de rozamiento.

El valor del coeficiente de rodadura es característico de cada sistema, dependiendo de:

  • la rigidez o dureza de la rueda y superficie,
  • el radio de la rueda (a mayor radio menor resistencia),
  • el peso o carga al que se somete cada rueda (en esto se diferencia del coeficiente de rozamiento),
  • en el caso de ruedas neumáticas o hidráulicas, de su presión (a mayor presión menor resistencia),
  • temperatura, el acabado de las superficies en contacto, velocidad relativa, etc.

Como ejemplo, para los cálculos de frenado en automóviles utilitarios, se utilizan valores de Crren torno a 0.012, y en trenes en torno a 0.0005.

Ejemplos de resistencia a la rodadura

Cuadro de resistencia a la rodadura: [1]

C_\text{rr}\, \mu_\text{r}\, Descripción
0,0002 a 0,0010[1] [2] 0.5 mm Ruedas de ferrocarril sobre railes de acero
0,1 mm Rodamientos de bolas en acero sobre acero
0,0025[3] Neumáticos especiales Michelin para automóvil solar/eco-marathon
0,005 Raíles estándar de tranvía
0,0055 Neumáticos BMX de bicicleta usados para automóviles solares[3]
0,006 a 0,01 Neumáticos de automóvil de baja resistencia y neumáticos de camión sobre carretera lisa
0,010 a 0,015[4] Neumáticos ordinarios de automóvil sobre hormigón
0,020 Neumáticos ordinarios de automóvil sobre losas de piedra
0,030 a 0,035 Neumáticos ordinarios de automóvil sobre alquitrán o asfalto
0.055 a 0.065 Neumáticos ordinarios de automóvil sobre hierba, barro y arena
0,3[4] Neumáticos ordinarios de automóvil sobre hierba, barro y arena

Por ejemplo, un automóvil de 1000 kg sobre una carretera asfaltada necesita una fuerza o empuje de aproximadamente 300 N para rodar (1000 kg × 9,81 m/s2 × 0,03 = 294,30 N).

Rodadura con y sin deslizamiento

La ecuación (4) da la respuesta la problema de qué fuerza horizontal es la mínima necesaria para que una fuerza horizontal pueda empezar a mover una rueda o cilindro. Otro problema relacionado con ese es si un determinado par aplicado por un eje motor sobre una rueda permitiría desplazar una cierta carga o si por el contrario la rueda patinaría ocasionando una situación de deslizamiento sin rodadura (tal como sucede por ejemplo cuando un automóvil trata de arrancar sobre hielo o sobre un suelo en el que existe un fluido lubricante). La condición necesaria para que haya rodadura sin deslizamiento es que:

\frac{\mu_{\text{r}}}{R} \le \mu

Donde:

\mu_{\text{r}}\,, es el coeficiente de resistencia a la rodadura.
\mu\, el coeficiente de rozamiento para deslizamiento.

Véase también

Referencias

  1. ↑ Gordon, David W. Bicycling Science. Cambridge, Mass. : MIT Press (c. 2004)
  2. ↑ Williams, John A. Engineering Tribology. New York : Cambridge University Press (2005)
  3. ↑ a b Roche, Schinkel, Storey, Humphris & Guelden, "Speed of Light." ISBN 0-7334-1527-X
  4. ↑ a b Gillespie ISBN 1-56091-119-9 p117

Bibliografía

  • Ortega, Manuel R. (1989-2006) (en español). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
  • Resnick, Robert & Halliday, David (2004) (en español). Física 4ª. CECSA, México.. ISBN 970-24-0257-3. 
  • Serway, Raymond A.; Jewett, John W. (2004) (en inglés). Physics for Scientists and Engineers (6ª edición). Brooks/Cole. ISBN 0-534-40842-7. 
  • Tipler, Paul A. (2000) (en español). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3. 

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Rodadura — Saltar a navegación, búsqueda Figura 1. Rodadura. El desplazamiento horizontal del cilindro es igual a la longitud del arco de ángulo central θ …   Wikipedia Español

  • Resistencia — Saltar a navegación, búsqueda Por resistencia puede entenderse: Contenido 1 En física e ingeniería 2 En fisiología 3 En medicina y en veterinaria …   Wikipedia Español

  • Resistencia — ► sustantivo femenino 1 Acción y resultado de resistir o resistirse. SINÓNIMO aguante 2 Capacidad para resistir: ■ los corredores de maratón tienen mucha resistencia. SINÓNIMO energía ANTÓNIMO debilidad 3 MECÁNICA Causa que se opone a la acc …   Enciclopedia Universal

  • Juntura — Junta de vía en rieles de perfil R50. En vías férreas, se denomina juntura o junta al sector de unión de los raíles o rieles. Constituye el punto débil de la vía, especialmente desde el punto de vista dinámico con el uso de eclisas aseguradas por …   Wikipedia Español

  • Fórmula 1 — Fórmula 1 …   Wikipedia Español

  • Suspensión de bicicleta — El Giant Innova de 2005 cuenta con suspensión delantera y trasera y además con una tija de sillín con suspensión y tija del manubrio ajustable. Una suspensión de la bicicleta es el sistema o sistemas utilizados para amortiguar el piloto y toda o… …   Wikipedia Español

  • AMC Amitron — Amitron Fabricante American Motors Corporation Período 1967 Fábricas Estados Unidos Sucesor Ninguno …   Wikipedia Español

  • Tuneo — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar al autor princip …   Wikipedia Español

  • SEAT Ronda — Fabricante SEAT Período 1982 1986 …   Wikipedia Español

  • Neumático — Estructura de un neumático sin cámara. 1. cinturón de acero en dirección longitudinal 2. estructura radial 3. alambre 4. llanta 5. banda de rodamiento 6. pared lateral 7. talón (ceja) Un neumático (del griego πνευματικός, relativo al pulmón, por… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”