Generatriz

La generatriz^[1] es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.^[2]

Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas, elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.

La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal.

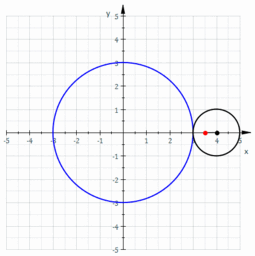En la figura, la circunferencia de color azul es la directriz, y la circunferencia de color negro es la generatriz. Un punto vinculado a ella describe una forma llamada epitrocoide: la curva de color rojo.

Curvas conformadas por circunferencias generatrices

• Cicloide, la curva plana generada por un punto de una circunferencia generatriz al rodar sobre una línea recta, sin deslizarse.
• Epicicloide, la curva que describe un punto vinculado a una circunferencia generatriz que rueda –sin deslizamiento– sobre una circunferencia directriz, tangencialmente.
• Hipocicloide, la curva que describe la trayectoria un punto situado sobre una circunferencia generatriz que rueda por el interior de otra circunferencia directriz, sin deslizamiento.

• Trocoide, la curva plana que describe un punto, vinculado a una circunferencia generatriz, que rueda sobre una línea recta directriz, tangencialmente, sin deslizamiento.
• Epitrocoide, la curva que describe un punto vinculado a una circunferencia generatriz que rueda –sin deslizamiento– sobre una circunferencia directriz, tangencialmente.
• Hipotrocoide, la curva plana que describe un punto vinculado a una circunferencia generatriz que rueda dentro de una circunferencia directriz, tangencialmente, sin deslizamiento.

Generatriz del cilindro

El cilindro es un cuerpo de revolución engendrado por un rectángulo al girar en torno a uno de sus lados, que será la altura del cilindro y el lado opuesto será la generatriz. Por tanto la altura del cilindro será igual a la generatriz.

h = g

Generatriz del cono

El cono es un cuerpo de revolución engendrado por un triángulo rectángulo al girar en torno a uno de sus catetos, que será la altura del cono y la hipotenusa será la generatriz.

Por el teorema de Pitágoras la generatriz del cono será igual a: g²=h²+r²

Generatriz del tronco de cono

El tronco de cono es un cuerpo de revolución engendrado por un trapecio rectángulo al girar en torno al lado perpendicular a las bases, que será la altura del cono y el otro lado será la generatriz.

Obtenemos la generatriz del tronco de cono aplicando el teorema de Pitágoras en el triángulo sombreado: g²=h²+(R-r)²

Véase también

• Hipocicloide
• Astroide
• Superelipse

Trolasso

Referencias