La conjunción de la falacia es una falacia lógica, que ocurre cuando es asumida en condiciones específicas que son más probables que una forma simple general.

El ejemplo más citado de esta falacia fue originó con los siguientes editores: Amos Tversky y Daniel Kahneman⁽¹⁾

“Linda tiene 31 años de edad, soltera, inteligente y muy brillante. Se especializó en filosofía. Como estudiante, ella estaba profundamente preocupada por los problemas de discriminación y justicia social, participando también en demostraciones anti-nucleares.”

¿Cual es más probable?

1. Linda es una cajera.
2. Linda es una cajera de banco y es activa en movimientos feministas.

El 85% de los encuestados eligió la opción 2⁽²⁾. Sin embargo, la probabilidad de que los dos eventos ocurran juntos (en "conjunción") es siempre menor o igual que la probabilidad de que ocurran juntos – formalmente los dos eventos A y B, esta desigualdad podría escribirse como:

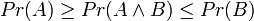
Por ejemplo, incluso escogiendo la más baja probabilidad de Linda siendo cajera de banco, se dice Pr (Linda es una cajera de banco) == 0.05 y una probabilidad alta que ella podría ser una feminista, de dice Pr (Linda es una feminista) = 0.95, entonces asumiendo en forma independiente que, Pr (Linda es un cajero de banco y Linda es una feminista) = 0.05 x 0.95 == 0.0475, inferior que Pr (Linda es una cajera de banco).

Tversky y Kahneman argumentan que la mayoría de las personas tienen este problema de manera incorrecta, porque ellos usan la representatividad heurística para tomar este tipo de sentencia: La opción 2 parece más "representativa" de que Linda se base sobre la descripción de ella, incluso aunque es claro que matemáticamente es menos probable.

Así como el caso, de que algunas personas pueden estar simplemente confundidas por la diferencia entre 'y' u 'o'. Tales confusiones son frecuentemente vistas en estos casos que no han sido estudiados en forma lógica; y, la probabilidad de tales sentencia usando "o" en lugar de “y” es completamente diferente. Ellos pueden manifestar que la sentencia N° 1 asume que Linda no necesariamente es activa en el movimiento feminista.

Muchas otras manifestaciones de este error han sido estudiadas. En otro experimento, como por ejemplo, policías expertos fueron encuestados del porcentaje de probabilidad que la Unión Soviética invadiera Polonia, y los Estados Unidos rompiera las relaciones diplomáticas a ocurrir en el siguiente año. Ellos lo razonaron sobre el promedio de que el 4% asumía la probabilidad de que esto ocurra. Otro grupo de expertos fueron encuestados para estimar la probabilidad simple que los Estados Unidos rompa relaciones con la Unión Soviética en el siguiente año, ellos le dieron un promedio de probabilidad solamente del 1%. Los investigadores argumentaron que en un escenario especifico parecía más seguro debido a la representatividad heurística, actualmente cada detalle que se añada seria un escenario menor; y, cada vez menos probable⁽³⁾ De este manera podría ser similar a la viveza engañosa ó pensamientos esquivos de la falacia, aunque es posible que las personas subestiman la posibilidad general de que un evento ocurra cuando no exista un escenario correcto para reflexionar.

Contenido 1 Una explicación cuántica de probabilidad de la Conjunción de la Falacia 2 Notas 3 Bibliografía

Una explicación cuántica de probabilidad de la Conjunción de la Falacia

En un reciente trabajo de Franco⁽⁴⁾ la Conjunción de la Falacia ha sido descrita en base al formalismo matemático de la mecánica cuántica. En particular, se ha demostrado que cada par de eventos mutuamente excluyentes (Linda es ó no es feminista, o Linda es ó no es una cajera) puede estar asociada a una base de un espacio vectorial de dos dimensiones.

Además, se supone que la realidad del sujeto acerca de estos acontecimientos se describen por un vector (llamado estado de opinión |s >), el cual puede ser escrito como una superposición de las bases vectoriales:
| s > = s₀ | a₀ > + s₁ | a₁ >

Donde | a₀ > y | a₁ >; son las bases vectoriales relevantes de una pareja particular de eventos mutuamente excluyentes (por ejemplo, Linda es o no una feminista). La probabilidad subjetiva relevante del evento a1 (Linda es feminista) es:
P(a₁) = | s₁ | ²
Si nosotros queremos describir la probabilidad subjetiva relevante para otro par de eventos mutuamente excluyentes b₀, b₁ (Linda es ó no una cajera), la ley de la probabilidad total se sustituye en el marco cuántico, por la siguiente ley:
P(b₁) = P(a₁)P(b₁ | a₁) + P(a₀)P(b₁ | a₀) + Interferencia
Donde el término de la interferencia (con una forma matemática precisa) tiene un rol muy importante en la Conjunción de la Falacia. De hecho, la presencia de términos de interferencia fuertemente negativos pueden ser P(b₁) < P(a₁)P(b₁ | a₁), que son precisamente la Conjunción de la Falacia (la probabilidad estimada que Linda es una cajera es inferior que la probabilidad estimada que Linda es feminista y también una cajera).

Un factor importante es que dentro de la mecánica cuántica, es imposible medir simultáneamente dos cantidades observadas. Por lo tanto, la probabilidad conjunta se sustituye por el concepto de probabilidades consecutivas; es decir:
P(a₁)P(b₁ | a₁)

En otras palabras, se ha demostrado que el uso de la probabilidad cuántica, permite describir de forma natural la Conjunción de la Falacia.

Notas

1. Tversky y Kahneman (1982, 1983)
2. Muchas variaciones de este experimento en la redacción y elaboración se han publicado cuando Tversky y Kahneman (1983) cambió la primera opción que "Linda es una cajera de banco o no es activa en el movimiento feminista"; en el mismo experimento, se ha descrito que la mayoría de los encuestados, todavía prefieren la segunda opción.
3. Tversky y Kahneman (1983)
4. Riccardo Franco (2007), La Conjunción de la Falacia y los efectos de la interferencia, http://arxiv.org/abs/0708.3948v1

Bibliografía

• Tversky, A. y Kahneman, D. (octubre de 1983). "Extensión versus razonamiento intuitivo: La Conjunción de la Falacia es una probabilidad de sentencia". Psychological Review 90 (4): 293-315. doi: 10.1037/0033-295X.90.4.293. http://content2.apa.org/journals/rev/90/4/293.

• Tversky, A. y Kahneman, D. (1982) "Sentencias de y por representatividades". En D. Kahneman, P. Slovic y A. Tversky (Eds.), Sentencia de incertidumbre: Heurística y sesgos. Cambridge, Reino Unido: Cambridge University Press.