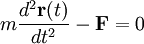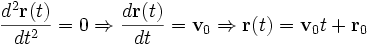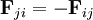- Dinámica del punto material
-
Dinámica del punto material
La dinámica del punto material es una parte de la mecánica newtoniana en la que los sistemas se analizan como sistemas de partículas puntuales y que se ejercen fuerzas a distancia instantáneas.
Contenido
Sistema de una sola partícula
Si se estudia el movimiento de una partícula material desde un sistema de referencia inercial, entonces la ecuación de movimiento básica es la segunda ley de Newton:
Donde r está representando la posición de la partícula, t es el instante del tiempo en que se mide la posición y F la fuerza. Si el sistema de una partícula está totalmente aislada de cualquier interacción con el exterior, no existirán fuerzas sobre la partícula y entonces la segunda ley de Newton se reduce a que:
Y por tanto la partícula se mueve a velocidad constante sobre una línea recta, tal como expresa la primera ley de Newton o ley de inercia. Y así cualquier magnitud física que, fijado un observador, dependa únicamente de la velocidad se mantendrá constante a lo largo del tiempo (para una partícula aislada eso sucede con la energía, el momento lineal y el momento angular, entre otras).Sistemas de partículas interactuantes
Un sistema de partículas N puntuales es un sistema algo más interesante, donde la segunda ley de Newton nos dice que la trayectoria de cada una de las partículas estará gobernada por las ecuaciones siguientes:
(1)
![m_i\frac{d^2\mathbf{r}_i(t)}{dt^2} -
\left[ \sum_{j\ne i} \mathbf{F}_{ji}(\mathbf{r}_i-\mathbf{r}_j) \right]= 0](/pictures/eswiki/51/3133a712b743d0634b6c36a1ae6cec43.png)
Donde ri(t) es la posición de la partícula i-ésima en el instante de tiempo t, Fji representa la fuerza que ejerce la partícula j sobre la partícula i. Este sistema puede resultar difícil de integrar mediante los métodos más sencillos de la mecánica clásica. Aunque el carácter determinista de la mecánica newtoniana queda asegurado por el hecho de que:
- fijadas unas condiciones iniciales para las posiciones y las velocidades,
- fijados ciertas condiciones de regularidad sobre la forma funcional de las fuerzas en función de las posiciones, y siempre y
- cuando podamos asegurar que no se producen colisiones triples existe solución única para el anterior sistema de ecuaciones.
Aun cuando no podamos integrar de manera sencilla el sistema de ecuaciones (), que tiene en tres dimensiones 6N grados de libertad cinemáticos, podemos encontrar algunas integrales de movimiento que reducen el problema.
Conservación de la energía
Cuando las fuerzas que se ejercen las partículas son conservativas puede verse que existen funciones llamadas funciones de potencial Vji tales que:[1]
(2)
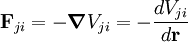
En ese caso puede probarse que a pesar de lo intricadas que puedan ser las trayectorias seguidas por las partículas, existe una magnitud física llamada energía total, que se conserva a lo largo del movimiento. Es decir, existe una función escalar cuyo valor se mantiene constante a lo largo del tiempo para el sistema, esta energía total viene dada por:
(3)
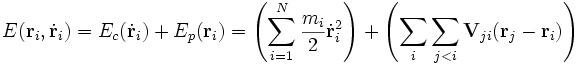
Para comprobar que esta magnitud permanece constante con el tiempo basta derivar la expresión () respecto al tiempo, y substituir dentro de la expresión obtenida ():
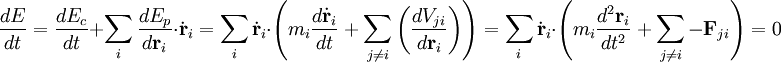
La expresión anterior se anula porque para todo i la expresión entre paréntesis es idénticamente nula, tal como muestra la ecuación del movimiento ().
Conservación del momento lineal
Otra ley de conservación que se menciona habitualmente en relación a los sistemas de partículas es la ley de conservación del momento lineal o cantidad de movimiento. En ciertos sistemas resulta que la magnitud vectorial obtenida como suma de momentos lineales:
(4)
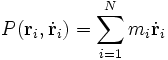
Permanece constante a lo largo del tiempo. Para que esa magnitud se conserve se requiere una condición sobre las fuerzas. Esta condición es el principio de acción-reacción fuerte que para un sistema de partículas implica:
En sistemas de partículas cargadas que interactúan entre sí mediante campos magnéticos, el momento lineal total de las partículas definido por () no cumple en general la anterior condición por lo que el momento lineal asociado a las partículas no se conserva. Sin embargo, si se considera el momento lineal que debe asignarse al campo electromagnético entonces puede escribirse una ley de conservación del momento para el sistema formado por el campo y las partículas (sin embargo, este momento total no vendría dado por ()).Casos particulares
- El problema de los dos cuerpos consiste en plantear un problema de tipo () con N = 2 es siempre resoluble ya que existen tantas integrales de movimiento como ecuaciones.
- El problema de los tres cuerpos es similar al anterior pero no puede construirse una solución a partir de integrales primeras, Poincaré probó un teorema que establece sólo existen 10 integrales de movimiento algebraicas en las coordenadas y momentos conjugados, lo cual imposibilita una solución por los medios usados para el problema de los dos cuerpos. Sin embargo, en 1912 Karl Fritiof Sundman halló una solución al problema de los tres cuerpos en forma de serie en potencias de
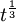que convergía lentamente para todo t y siempre y cuando el momento angular total no fuera cero. Sin embargo, esta solución converge muy lentamente y no resulta de un gran interés práctico.
- Un gas encerrado en una caja es otro interesante problema de partículas que puede ser analizado por la mecánica clásica. Sabemos que si todos los choques contra las paredes y entre partículas son perfectamente elásticos y el conjunto de puntos de la superficie de la caja que no presenta curvatura tiene medida de Lebesgue nula entonces el sistema es ergódico.
Referencia
- ↑ Landau y Lifshitz, pp. 15-17.
Bibliografía
- Landau & Lifshitz: Mecánica, Ed. Reverté, Barcelona, 1991. ISBN 84-291-4081-6.
Categorías: Mecánica newtoniana | Dinámica
Wikimedia foundation. 2010.
