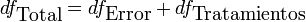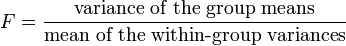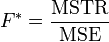En estadística, un experimento factorial completo es un experimento cuyo diseño consta de dos o más factores, cada uno de los cuales con distintos valores o "niveles", y cuyas unidades experimentales cubren todas las posibles combinaciones de esos niveles en todo los factores. Este tipo de experimentos permiten el estudio del efecto de cada factor sobre la varible respuesta, así como el efecto de las interacciones entre factores sobre la dicha variable.

Por ejemplo, con dos factores y dos niveles en cada factor, un experimento factorial tendría en total cuatro combinaciones de tratamiento, y se le denominaría diseño factorial de 2×2.

Si el número de combinaciones en un diseño factorial completo es demasiado alto parsu procesamiento, puede optarse por un diseño factorial fraccional, en el que seomitan algunas de las combinaciones posibles.

Contenido 1 Historia 2 Ejemplo Real 3 Notación 4 Analisis de Yates 5 Prueba F de Fisher 6 Referencias 7 Veáse también

Historia

Los diseños factoriales fueron utilizados en el siglo XIX por Jhon Bennet Lawes y Henri J Gilbert de la Estación experimental de Rothamsted.[1] Ronald Fisher discutió en 1926 que los diseños “complejos” (tales como diseños factoriales) eran más eficientes que estudiando un factor a la vez.[2] Fisher escribió, “ningún aforismo se repite más con frecuencia con respecto a ensayos prácticos, que eso nosotros debe hacer naturaleza pocas preguntas, o, idealmente, a una pregunta, a la vez. Convencen el escritor de que esta visión está confundida enteramente. Naturaleza, él sugiere, responderá lo más mejor posible a un lógico y pensó cuidadosamente hacia fuera el cuestionario ". Un diseño factorial permite el efecto de varios factores e incluso interacciones entre ellas que se determinarán con el mismo número de ensayos que son necesario determinar de los efectos por sí mismo con el mismo grado de exactitud.

Yates realizo importantes contribuciones significativas hechas, particularmente en el análisis de diseños, por Análisis de Yates. El término “factorial” no se pudo haber utilizado en la impresión antes de 1935, cuando el pescador la utilizó en su libro El diseño de experimentos. [1]

Ejemplo Real

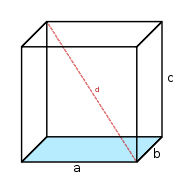
El experimento factorial más simple contiene dos niveles para cada uno de dos factores. Suponga los deseos de un ingeniero para estudiar la energía total usada por cada uno de dos diversos motores, A y B, funcionando en cada uno de dos diversas 2000 o 3000 RPM de las velocidades. El experimento factorial consistiría en cuatro elementos experimentales: viaje en automóvil A en 2000 RPM, viaje en automóvil B en 2000 RPM, viaje en automóvil A en 3000 RPM, y viaje en automóvil B en 3000 RPM. Cada combinación de un solo nivel seleccionado de cada factor está presente una vez. Este experimento es un ejemplo de 22 (o 2x2) experimento factorial, nombrado así porque considera dos niveles (la base) para cada uno de dos factores (la energía o el exponente), o #lniveles#factores, produciendo 22puntos factoriales =4. Los diseños pueden implicar muchas variables independientes. Como otro ejemplo, los efectos de tres variables entradas se pueden evaluar en ocho condiciones experimentales demostradas como las esquinas de un cubo. Esto se puede conducir con o sin la réplica, dependiendo de su propósito previsto y recursos disponibles. Proporcionará los efectos de las tres variables independientes en la variable dependiente y las interacciones posibles(en caso de haber mas de 3 se habla de un hiperespacio).

Notación

Para ahorrar el espacio, los puntos en un experimento factorial de dos niveles se abrevian a menudo con las cadenas de más y signos de menos. Las secuencias tienen tantos símbolos como factores, y sus valores dictan el nivel de cada factor: convencionalmente, − para el primer (o bajo) llano, y + para el segundo (o alto) llano. Los puntos en este experimento se pueden representar así como − − , + − , − + , y + + .

Los puntos factoriales se pueden también abreviar cerca (1), a, b, y el ab, donde la presencia de una letra indica que el factor especificado está en su alto (o en segundo lugar) nivel y la ausencia de una letra indica que el factor especificado está en su (o primero) nivel bajo (por ejemplo, “a” indica que el factor A está en su alto ajuste, mientras que el resto de los factores están en su ajuste del punto bajo (o primero)). (1) se utiliza indicar que todos los factores están en sus (o primero) valores más bajos.

Para poder finalmente obtener un modelo estadistico que nos indique el valor de respuesta al modificar los factores .

Calculo del efecto

Contraste = (suma de niveles+)-(suma de niveles-) Efecto Contraste /replica*2^k

b= efecto/2 bo= suma total/numero total

Modelo estadístico: Y= bo+ b1X1 + b2X2......

Analisis de Yates

La técnica fundamental es el repartir del total suma de cuadrados en componentes se relacionó con los efectos usados en el modelo. Por ejemplo, demostramos el modelo para un ANOVA simplificado con un tipo de tratamiento en diversos niveles.

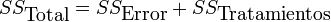
El número de los grados de libertad se puede repartir de una manera similar y especifican distribuciones chi-cuadrado que describen las sumas asociadas de cuadrados.

Prueba F de Fisher

Se utiliza para las comparaciones de los componentes de la desviación total. Por ejemplo, en una forma, o el solo-factor ANOVA, la significación estadística es probada para comparando la estadística de la prueba de F

donde:

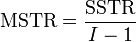, I = número de tratamientoss

y:

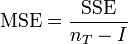, n_T = número total de casos

a F-distribución con el del I-1, secundario< del > n< T> /sub grados de libertad. Usar la F-distribución es un candidato natural porque la estadística de la prueba es el cociente de dos sumas malas de los cuadrados que tienen a distribución del chi-cuadrado.

Referencias

1.-Frank Yates and Kenneth Mather (1963). "Ronald Aylmer Fisher". Biographical Memoirs of Fellows of the Royal Society of London 9: 91–120. http://digital.library.adelaide.edu.au/coll/special//fisher/fisherbiog.pdf.

2.-Ronald Fisher (1926). "The Arrangement of Field Experiments". Journal of the Ministry of Agriculture of Great Britain 33: 503–513. http://digital.library.adelaide.edu.au/coll/special//fisher/48.pdf.

Veáse también

• Anova