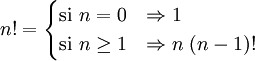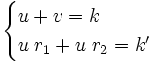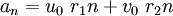Anuncio de cacao con una imagen recursiva. La mujer muestra un paquete idéntico al del propio anuncio, conteniendo así a otra mujer que muestra otro paquete más pequeño, de forma recursiva.

Imagen recursiva formada por un triángulo. Cada triángulo está compuesto de otros más pequeños, compuestos a su vez de la misma estructura recursiva.

Recursión o recursividad es la forma en la cual se especifica un proceso basado en su propia definición. Siendo un poco más precisos, y para evitar el aparente círculo sin fin en esta definición:

Un problema que pueda ser definido en función de su tamaño, sea este N, pueda ser dividido en instancias más pequeñas (< N) del mismo problema y se conozca la solución explícita a las instancias más simples, lo que se conoce como casos base, se puede aplicar inducción sobre las llamadas más pequeñas y suponer que estas quedan resueltas.

Para que se entienda mejor a continuación se exponen algunos ejemplos:

• Factorial(x: Entero): Sea N := x el tamaño del problema, podemos definir el problema de forma recurrente como x*Factorial(x - 1); como el tamaño de Factorial(x - 1) es menor que N podemos aplicar inducción por lo que disponemos del resultado. El caso base es el Factorial(0) que es 1.

• Ordenación por fusión(v: vector): Sea N := tamaño(v), podemos separar el vector en dos mitades. Estas dos mitades tienen tamaño N/2 por lo que por inducción podemos aplicar la ordenación en estos dos subproblemas. Una vez tenemos ambas mitades ordenadas simplemente debemos fusionarlas. El caso base es ordenar un vector de 0 elementos, que está trivialmente ordenado y no hay que hacer nada.

En estos ejemplos podemos observar como un problema se divide en varias (>= 1) instancias del mismo problema, pero de tamaño menor gracias a lo cual se puede aplicar inducción, llegando a un punto donde se conoce el resultado (el caso base)..

Nota: aunque los términos "recursión" y "recursividad" son ampliamente empleados en el campo de la informática, el término correcto en castellano es recurrencia. Sin embargo este último término es algo más específico. Véase relación de recurrencia.

Los números naturales

Un ejemplo de conjunto definido de forma recurrente es el de los números naturales:

a) 0 pertenece a N

b) Si n pertenece a N, entonces n+1 pertenece a N

c) Si X verifica a) y b) , entonces N está incluido en X

Los números naturales es el conjunto de números enteros no negativos.

Funciones definidas de forma recurrente

Aquellas funciones cuyo dominio puede ser recursivamente definido pueden ser definidas de forma recurrente.

El ejemplo más conocido es la definición recurrente de la función factorial n!:

Con esta definición veamos como funciona esta función para el valor del factorial de 3:

3! = 3 · (3-1)!
   = 3 · 2!
   = 3 · 2 · (2-1)!
   = 3 · 2 · 1!
   = 3 · 2 · 1 · (1-1)!
   = 3 · 2 · 1 · 0!
   = 3 · 2 · 1 · 1
   = 6

Algoritmo recurrente

Un método usual de simplificación de un problema complejo es la división de este en subproblemas del mismo tipo. Esta técnica de programación se conoce como divide y vencerás y es el núcleo en el diseño de numerosos algoritmos de gran importancia, así como también es parte fundamental de la programación dinámica.

El ejemplo del cálculo recursivo del factorial de un número llevado al campo de la programación, en este ejemplo C++:

int factorial (int x)
{
  if (x < 2) return 1; // Caso base: Cuando X < 2 devolvemos 1 puesto que 1! = 1
  return x*factorial(x - 1); // Si X >= 2 devolvemos el producto de 'X' por el factorial de 'X'-1
}

El seguimiento de la recursividad programada es casi exactamente igual al ejemplo antes dado, para intentar ayudar a que se entienda mejor se ha acompañado con muchas explicaciones y con colores que diferencia los distintos sub-procesos de la recursividad.

X = 3 //Queremos 3!, por lo tanto X inicial es 3
X >= 2 -> return 3*factorial(2);
    X = 2 //Ahora estamos solicitando el factorial de 2
    X >= 2 -> return 2*factorial(1);
        X = 1 // Ahora estamos solicitando el factorial de 1
        X < 2 -> return 1;
        [En este punto tenemos el factorial de 1 por lo que volvemos marcha atrás resolviendo todos los resultados]
    return 2 [es decir: return 2*1 = return 2*factorial(1)]
return 6 [es decir: return 3*2 = return 3*factorial(2)*factorial(1)] // El resultado devuelto es 6

Ejemplos de recurrencias

Resolución de ecuaciones homogéneas de primer grado, segundo orden:

a) Se pasan al primer miembro los términos a_n, a_{n − 1}, a_{n − 2}, los cuales también podrían figurar como a_{n + 2}, a_{n + 1}, a_n

b) Se reemplaza a_n por r², a_{n − 1} por r y a_{n − 2} por 1, quedando una ecuación de segundo grado con raíces reales y distintas r₁ y r₂.

c) Se plantea

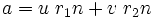
d) Debemos tener como dato los valores de los dos primeros términos de la sucesión: 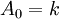y 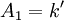. Utilizando estos datos ordenamos el sistema de 2x2:

La resolución de este sistema nos da como resultado los valores u₀ y v₀, que son números reales conocidos.

e) La solución general es:

Algunos ejemplos de recurrencia:

• Factorial -- n! = n × (n-1)!
• Sucesión de Fibonacci -- f(n) = f(n-1) + f(n-2)
• Números de Catalan -- C(2n, n)/(n+1)
• Las Torres de Hanoi
• Función de Ackermann

Véase también

• Algoritmo recursivo
• Fractal
• Sistema-L

Enlaces externos

• Ejemplo de curvas recursivas fractales