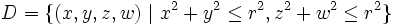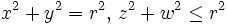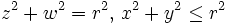- Duocilindro
-
Duocilindro
El duocilindro es un objeto de revolución del espacio tetradimensional. Se describe como el producto cartesiano de dos discos definidos sobre los planos XY y ZW del espacio tetradimensional euclídeo.
Contenido
Geometría
El duocilindro está limitado por dos variedades de dimensión 4 que son perpendiculares entre sí. Las variedades proyectan un toroide en el espacio de 3 dimensiones, y están descritas de la siguiente forma:
Las proyecciones del duocilindro que son paralelas en el espacio tridimensional son cilindros. Las proyecciones en perspectiva generan figuras con forma de toroide.
El duocilindro es la figura que de forma cuando el número de lados de los polígonos que forman los prismas de un duoprisma tiende a infinito.
Intersección con el espacio tridimensional
La intersección del duocilindro con nuestro espacio es un cilindro, siempre que pase paralela o perpendicularmente a uno de sus discos. Imaginemos ahora que un duocilindro va a cruzar nuestro espacio de ésa forma: En el momento justo la intersección con nuestro espacio el resultado es un círculo, un cilindro de altura infinitesimal. Conforme va atravesando nuestro espacio, la altura del cilindro resultante va aumentando hasta alcanzar una altura máxima en la mitad del cruce. Luego la altura del cilindro va disminuyendo hasta desaparecer.
Propiedades
Un duocilindro puede rodar sobre una superficie en el espacio tetradimensional, igual que el cilindro y el círculo pueden rodar en el espacio de 3 y 2 dimensiones. La mayor diferencia reside en que el duocilindro tiene dos 'superficies' capaces de rodar que son perpendiculares entre sí. Cuando el duocilindro rueda, puede cubrir el espacio de una recta; y si se 'coge' y se le pone sobre su otra superficie rodante cubrirá el espacio de otra recta perpendicular a la anterior.
El duocilindro tiene un volumen de 4π2r3 y un tetravolumen de π2r4.
Referencias
Categoría: Geometría tetradimensional
Wikimedia foundation. 2010.