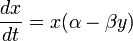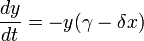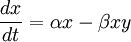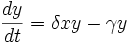Las ecuaciones de Lotka-Volterra, también conocidas como ecuaciones predador-presa, son un par de ecuaciones diferenciales de primer orden no lineales que se usan para el modelado de dos poblaciones que interactuan, una presa y un depredador. Las ecuaciones fueron propuestas de forma independiente por Alfred J. Lotka en 1925 y Vito Volterra en 1926.

Tales ecuaciones se definen como:

donde

• y es el número de algún predador (por ejemplo, un lobo);
• x es el número de sus presas (por ejemplo, conejos);
• dy/dt y dx/dt representa el crecimiento de las dos poblaciones en el tiempo;
• t representa el tiempo; y
• α, β, γ y δ son parámetros que representan las interacciones de las dos especies.

Contenido 1 Explicación de las ecuaciones 1.1 Presa 1.2 Depredador 2 Enlaces externos

Explicación de las ecuaciones

Usando las series de Taylor obtenemos una solución lineal a las ecuaciones:

f(x,y) = A₀ − A₁x − A₂y

g(x,y) = B₀ + B₁x − B₂y.

Con estos coeficientes se puede estudiar los modelos de competición, enfermedad y mutualismo_(biología) en un ecosistema.

Presa

Se asume que las presas tienen suministro de comida ilimitado, y se reproducen exponencialmente a menos que exista algún predador. Este crecimiento exponencial está representado en la ecuación por el término αx. El termino de la ecuación βxy viene a representar el encuentro de las dos especies y su interacción. Si x o y son cero no existe interacción.

Podemos interpretar la ecuación como el cambio del número de presas viene dado por su propio crecimiento menos la tasa de encuentros con predadores.

Depredador

En esta ecuación, δxy representa el crecimiento de los depredadores (fíjese en la similitud con la ecuación para las presas, pero en este caso para el crecimiento de los depredadores es necesario usar la razón a la que se consumen las presas, x). γy representa la muerte natural de los depredadores de forma exponencial; a más depredadores es necesario que el número de presas aumente para mantener la población.

Podemos interpretar la ecuación como el crecimiento de los depredadores por la caza de presas menos la muerte natural de éstos.

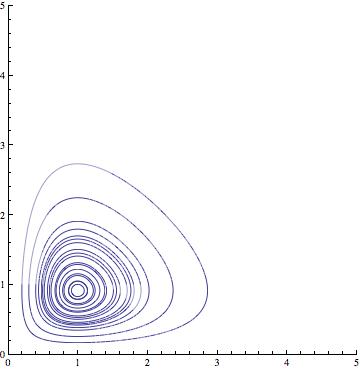
Enlaces externos

• Lotka-Volterra Predator-Prey Model by Elmer G. Wiens
• Lotka-Volterra Model
• [1] NANIA Lotka-Volterra applet