Ecuación diferencial ordinaria de primer orden

Ecuación diferencial ordinaria de primer orden

Ecuación diferencial ordinaria de primer orden

Una ecuación diferencial ordinaria de primer orden es una ecuación diferencial ordinaria dónde intervienen derivadas de primer orden respecto a una variable independiente. Estas ecuaciones, junto con su condición inicial, se pueden encontrar expresadas en forma explícita:

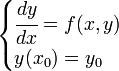
(1a) \begin{cases} \cfrac{dy}{dx} = f(x,y) \\ y(x_0) = y_0 \end{cases}

o en su forma implícita:

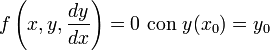
(1b) f\left(x,y,\frac{dy}{dx}\right) = 0\ \mbox{con}\ y(x_0) = y_0

Contenido

Ejemplos de ecuaciones diferenciales de primer orden

Ecuaciones de variables separables

Si mediante operaciones algebraicas es posible expresar la ecuación diferencial en la siguiente forma:

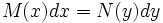
(2a) M(x) dx = N(y) dy\;

se dirá que es una ecuación diferencial de variables separables. De este modo, en cada miembro de la ecuación se tendrá una única variable. Para resolver este tipo de ecuaciones basta con integrar en cada miembro:

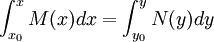
(2b) {\int_{x_0}^{x} M(x)dx}={\int_{y_0}^{y} N(y)dy}

Ecuaciones homogéneas

Se dice que una ecuación es homogénea si la función f(x, y) es fraccionaria y además el grado de los polinomios de numerador y denominador son los mismos. Por ejemplo:

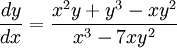
\frac{dy}{dx} =\frac{x^2y+y^3-xy^2}{x^3-7xy^2}

sería homogénea ya que todos los términos de ambos polinomios son de grado 3. Así se procede dividiendo tanto numerador como denominador por x3 o y3 en función de qué cambio haga más simple su resolución. Llegados a este caso según la elección se puede optar por uno de los dos cambios análogos, que son:

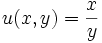u(x,y) = \frac{x}{y} o bien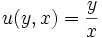 u(y,x) = \frac{y}{x}

Así se simplifica enormemente y suele quedar separable. Para finalizar solo resta deshacer el cambio, sustituyendo las u(x,y) por su valor como función que se ha establecido.

El caso anterior puede generalizarse a una ecuación diferencial de primer orden de la forma:

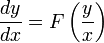
(3a) \frac{dy}{dx} = F\left( \frac{y}{x} \right)

introduciendo la variable u = y/x; la solución de la anterior ecuación viene dada por:

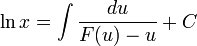
(3b) \ln x = \int \frac{du}{F(u)-u}+C

Ecuaciones lineales de primer orden

La ecuación diferencial lineal de primer orden tiene la forma:

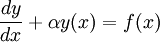
(4a) \frac{dy}{dx} + \alpha y(x) = f(x)

Y la solución de la misma viene dada por:

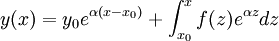
(4b) y(x) = y_0 e^{\alpha(x-x_0)}+ \int_{x_0}^x f(z)e^{\alpha z} dz

Ecuación diferencial de Bernoulli

Una ecuación de Bernoulli es aquella que tiene la forma:

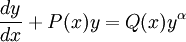
(5a) \frac{dy}{dx} + P(x)y = Q(x) y^\alpha

Donde P(x) y Q(x) son funciones continuas cualesquiera. Su solución para α > 1 viene dada por:

(5b) y(x)={\frac {{e^{-\int \!P \left( x \right) {dx}}}}{\sqrt [\alpha-1]{ \left( 1-\alpha \right) \int \!Q \left( x \right) {dx}+C}}}

Véase también

Obtenido de "Ecuaci%C3%B3n diferencial ordinaria de primer orden"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Ecuación diferencial ordinaria — Saltar a navegación, búsqueda En matemáticas, una ecuación diferencial ordinaria (comúnmente abreviada EDO ) es una relación que contiene funciones de una sola variable independiente, y una o más de sus derivadas con respecto a esa variable. Las… …   Wikipedia Español

  • Ecuación diferencial exacta — Saltar a navegación, búsqueda En matemáticas, una ecuación diferencial exacta es una ecuación diferencial ordinaria de primer orden que presenta la forma: en donde las derivadas parciales de las funciones M y N: y son iguales. Esto es equivalente …   Wikipedia Español

  • ecuación diferencial ordinaria — Ecuación que contiene derivadas de una función de una sola variable. Su orden es el de la derivada de mayor orden que contiene (p. ej., una ecuación diferencial de primer orden involucra sólo la primera derivada de la función). Debido a que la… …   Enciclopedia Universal

  • Ecuación diferencial lineal — Saltar a navegación, búsqueda Una ecuación diferencial lineal ordinaria es una ecuación diferencial que tiene la forma general y comprensible de escribir la ecuación es de la siguiente forma: O usando otra notación frecuente …   Wikipedia Español

  • Ecuación diferencial — Saltar a navegación, búsqueda Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se… …   Wikipedia Español

  • Ecuación diferencial de Bernoulli — Saltar a navegación, búsqueda Las ecuaciones diferenciales de Bernoulli son ecuaciones diferenciales ordinarias de primer orden, formuladas por Jakob Bernoulli y resueltas por su hermano Johann, que se caracterizan por tener la forma: donde y …   Wikipedia Español

  • Ecuación en derivadas parciales — Saltar a navegación, búsqueda En matemáticas una ecuación en derivadas parciales (a veces abreviado como EDP) es una relación entre una función u de varias variables independientes x,y,z,t,... y las derivadas parciales de u respecto de esas… …   Wikipedia Español

  • Formulación débil de una ecuación diferencial — La formulación débil (o formulación variacional) de un problema definido mediante ecuaciones diferenciales es una forma alternativa en que dichas ecuaciones se escriben en forma integral, dando lugar a ecuaciones tratables mediante los métodos… …   Wikipedia Español

  • Ecuación de Riccati — Saltar a navegación, búsqueda La ecuación de Riccati es una ecuación diferencial ordinaria desarrollada en el siglo XVIII por el matemático italiano Jacopo Francesco Riccati, con el fin de analizar la hidrodinámica. Corresponde a una ecuación de… …   Wikipedia Español

  • Ecuación — (Derivado culto de aequare, igualar.) ► sustantivo femenino 1 MATEMÁTICAS Igualdad entre dos expresiones que contienen una o más incógnitas: ■ para resolver la ecuación despeja primero la incógnita. 2 ASTRONOMÍA Diferencia que hay entre el lugar… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”