Ecuaciones de Cauchy-Riemann

Ecuaciones de Cauchy-Riemann

Ecuaciones de Cauchy-Riemann

Las ecuaciones de Cauchy-Riemann son dos ecuaciones diferenciales parciales que son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria (aunque no suficiente) para la derivabilidad de este tipo de funciones.

Sea una función compleja f(z), con z = x + iy. Se sabe que f(z) se puede descomponer en suma de dos funciones reales de dos variables u y v, de manera que f(z) = f(x,y) = f(x + iy) = u(x,y) + iv(x,y). Si la función f(z) es derivable en un punto z0 = x0 + iy0 entonces deben verificarse las condiciones de Cauchy-Riemann:

ux(x0,y0) = vy(x0,y0)

vx(x0,y0) = − uy(x0,y0)


donde ux significa la derivada parcial de la función u respecto a la variable x, usualmente simbolizado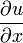 \frac{\partial u}{\partial x} . Análogamente para uy, vx y vy.

Además se cumple que el valor de la derivada en el punto, de existir, debe ser:

f'(z0) = ux(x0,y0) + ivx(x0,y0) = vy(x0,y0) − iuy(x0,y0)

Contenido

Ejemplo

Veamos un ejemplo donde derivable en todo número complejo y por lo tanto las ecuaciones de Cauchy-Riemann se verificarán en cualquier z = x + iy. Consideramos la función f(z) = z2. Ahora veamos esta función en coordenadas cartesianas.

f(x + yi) = (x + yi)2 = (x2 − y2) + i2xy

por lo tanto las parte real e imaginaria de la función son u(x,y) = x2 − y2 y v(x,y) = 2xy respectivamente. Derivado con respecto a x e y es inmediato que

ux = 2x = vy

y que

uy = − 2y = − vx.

Por último verifiquemos la condición sobre las derivadas. La derivada (ver Complex analysis) de f es claramente f'(z) = 2z (las reglas para derivar funciones complejas es similar a las funciones reales) por lo tanto

f'(x + iy) = 2(x + iy) = 2x + i2y = ux + ivx = vy − iuy

Otras formas de expresar las ecuaciones

Algunas formas equivalentes de expresar las condiciones de Cauchy-Riemann son las siguientes:

fx + ify = 0

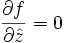
\frac{\partial f}{\partial \hat{z}}=0

Observación

Hay que hacer notar que las ecuaciones de Cauchy-Riemann no constituyen una condición suficiente, por lo que no valen por sí solas para demostrar la derivabilidad de una función en un punto.

Sin embargo, sí tenemos condiciones suficientes de derivabilidad si la función, además de cumplir las ecuaciones de Cauchy-Riemann, se puede descomponer en dos funciones u y v con derivadas parciales primeras continuas en un entorno de z0 = (x0,y0).

Aplicación

Se dice que una función de armónica cuando verifica la ecuación de Laplace:

hxx + hyy = 0.

No es difícil verificar que dos funciones de clase C2 que verifiquen las condiciones de Cauchy-Riemann son ambas armónicas. En tal caso se dice que ellas son armónicas conjugadas.

Enlaces externos

Obtenido de "Ecuaciones de Cauchy-Riemann"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Ecuaciones de Cauchy-Riemann — Las ecuaciones de Cauchy Riemann son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria para la derivabilidad de este tipo de funciones. Sea una función compleja ,… …   Enciclopedia Universal

  • Teorema de Cauchy — Numerosos teoremas deben su nombre a Augustin Louis Cauchy: El teorema integral de Cauchy en análisis complejo, generalizado al teorema de Cauchy Goursat. Véase también la fórmula integral de Cauchy. El teorema del valor medio de Cauchy en… …   Wikipedia Español

  • Bernhard Riemann — Para otros usos de este término, véase Riemann (desambiguación). Bernhard Riemann Bernhard Riemann, 1863 Nacimiento …   Wikipedia Español

  • Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… …   Wikipedia Español

  • Logaritmo complejo — Una única rama del logaritmo complejo. El tono del color se utiliza para mostrar el argumento (ángulo de coordenadas polares) del logaritmo complejo. La intensidad del color se utiliza para mostrar el módulo del logaritmo complejo. La página con… …   Wikipedia Español

  • Función holomorfa — Las funciones holomorfas son el principal objeto de estudio del análisis complejo; son funciones que se definen sobre un subconjunto abierto del plano complejo C y con valores en C, que además son complejo diferenciables en cada punto. Esta… …   Wikipedia Español

  • Variedad compleja — En geometría diferencial, una variedad compleja M es una variedad topológica que tiene la estructura que nos permite definir la noción de función holomorfa .[1] Ello se podrá conseguir por dos caminos: Exigiendo que exista un atlas (o conjunto de …   Wikipedia Español

  • Teorema de los residuos — El Teorema de los residuos es consecuencia directa del Teorema integral de Cauchy y forma parte fundamental de la teoría matemática de Análisis Complejo. Contenido 1 Enunciado 2 Demostración 3 Véase también …   Wikipedia Español

  • Función armónica — En matemáticas, sea f : D → R (donde D es un subconjunto abierto de Rn) una función real de n variables, se la llama armónica en D si sobre D tiene derivadas parciales continuas de primer y segundo orden y satisfacen la ecuación de Laplace… …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”