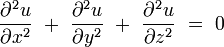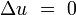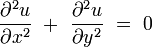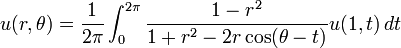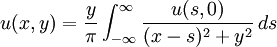Ecuación de Laplace

Ecuación de Laplace

Ecuación de Laplace

En cálculo vectorial, la ecuación de Laplace es una ecuación en derivadas parciales de segundo orden de tipo elíptico, que recibe ese nombre en honor al físico y matemático Pierre-Simon Laplace.

Introducida por las necesidades de la mecánica newtoniana, la ecuación de Laplace aparece en muchas otras ramas de la física teórica como la astronomía, la electrostática, la mecánica de fluidos o la mecánica cuántica.

Contenido

Definición

La ecuación de Laplace se define como:

Δu = 0

donde Δ es el operador laplaciano, y u; son funciones reales o complejas.

La ecuación de Laplace se trata de un caso particular de la ecuación de Poisson:

Δu = f cuando la función f es cero.

A las funciones soluciones de la ecuación de Laplace se les llama funciones armónicas.

Condiciones iniciales

El problema de Cauchy para la ecuación de Laplace se denomina un problema planteado no correctamente, puesto que la solución no depende continuamente de los datos del problema. Estos problemas mal definidos no son usualmente satisfactorios para las aplicaciones físicas.

Condiciones de frontera

Problema de Dirichlet

El problema de Dirichlet consiste en hallar una función armónica dados sus valores en la frontera de un dominio acotado. Esto es:

hallar una función u con primera y segunda derivadas continuas en D y continua en la frontera de D

Δu = 0 en D
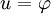u = \varphi en la frontera de D

para cierta función 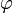\varphi continua en la frontera de D.

Como consecuencia del principio fuerte del máximo de las funciones armónicas se tiene que la solución del problema de Dirichlet si existe es única.

Ecuación de Laplace tridimensional

En coordenadas cartesianas, en un espacio euclídeo de tres dimensiones, el problema consiste en encontrar todas las funciones de tres variables reales 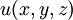u(x,y,z) \,\! que verifican la ecuación en derivadas parciales de segundo orden:

\frac{\partial^2 u}{\partial x^2} \ + \ \frac{\partial^2 u}{\partial y^2} \ + \ \frac{\partial^2 u}{\partial z^2} \ = \ 0

Para simplificar la escritura, se introduce el operador diferencial 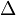\Delta \,\! (operador laplaciano) tal que la ecuación nos queda:

\Delta u \ = \ 0

Ecuación de Laplace bidimensional

En coordenadas cartesianas, en un espacio euclídeo de dos dimensiones, el problema consiste en encontrar todas las funciones de dos variables reales u(x,y) que verifican:

\frac{\partial^2 u}{\partial x^2} \ + \ \frac{\partial^2 u}{\partial y^2} \ = \ 0

Problema de Dirichlet

Problema de Dirichlet en el círculo unidad

Por la fórmula integral de Poisson tenemos que la solución al problema en un círculo (expresando la solución en coordenadas polares) es:

u(r, \theta) = {1\over 2 \pi} \int _0^{2\pi} {1 - r^2\over 1 + r^2 - 2 r \cos (\theta - t) } u (1,t)\, d t \;

Problema de Dirichlet en el semiplano superior

Se obtiene la conocida como fórmula integral de Schwartz:

u(x,y) = {y\over \pi} \int_{-\infty}^\infty {u(s,0)\over (x-s)^2 + y^2} \, d s \;

Véase también

Obtenido de "Ecuaci%C3%B3n de Laplace"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Ecuación en derivadas parciales — Saltar a navegación, búsqueda En matemáticas una ecuación en derivadas parciales (a veces abreviado como EDP) es una relación entre una función u de varias variables independientes x,y,z,t,... y las derivadas parciales de u respecto de esas… …   Wikipedia Español

  • Laplace — Laplace, Pierre Simón, marqués de Laplace, ecuación diferencial de Laplace, leyes de Laplace, transformada de * * * (as used in expressions) Laplace, ecuación de Laplace, Pierre Simon, marqués de …   Enciclopedia Universal

  • Ecuación de Poisson — Saltar a navegación, búsqueda En matemática y física, la ecuación de Poisson es una ecuación en derivadas parciales con una amplia utilidad en electrostática, ingeniería mecánica y física teórica. Su nombre se lo debe al matemático, geómetra y… …   Wikipedia Español

  • Ecuación elíptica en derivadas parciales — Saltar a navegación, búsqueda Una ecuación eliptica en derivadas parciales de segundo orden es una ecuación diferencial parcial del tipo en la cual la matriz es definida positiva. Un ejemplo de una ecuación diferencial parcial elíptica es la… …   Wikipedia Español

  • Ecuación — (Derivado culto de aequare, igualar.) ► sustantivo femenino 1 MATEMÁTICAS Igualdad entre dos expresiones que contienen una o más incógnitas: ■ para resolver la ecuación despeja primero la incógnita. 2 ASTRONOMÍA Diferencia que hay entre el lugar… …   Enciclopedia Universal

  • ecuación diferencial parcial — En matemática, una ecuación que contiene derivadas parciales, y que expresa un proceso de cambio que depende de más de una variable independiente. Puede ser leída como una afirmación sobre cómo evoluciona un proceso sin especificar la función… …   Enciclopedia Universal

  • Laplace, Pierre-Simon, marqués de — (23 mar. 1749, Beaumount en Auge, Franciandash–5 mar. 1827, París). Matemático, astrónomo y físico francés. Se lo conoce principalmente por sus investigaciones sobre la estabilidad del sistema solar y su teoría de la propagación de ondas… …   Enciclopedia Universal

  • Ecuación diferencial — Saltar a navegación, búsqueda Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se… …   Wikipedia Español

  • Laplace, ecuación de — En matemática, una ecuación diferencial parcial cuyas soluciones (funciones armónicas) son útiles en la investigación de problemas físicos en tres dimensiones que involucran campos gravitacionales, eléctricos y magnéticos, y ciertos tipos de… …   Enciclopedia Universal

  • Ecuación de Van der Waals — La ecuación de Van der Waals es una ecuación de estado de un fluido compuesto de partículas con un tamaño no despreciable y con fuerzas intermoleculares, como las fuerzas de Van der Waals. La ecuación, cuyo origen se remonta a 1873, debe su… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”