Las ecuaciones de Jefimenko describen el comportamiento de los campos eléctrico y magnético en función de la posición de las fuentes del campo en instantes retardados. Junto con la ecuación de continuidad, las ecuaciones de Jefimenko (1) son equivalentes a las ecuaciones de Maxwell.

Campo electromagnético en el vacío

El campo eléctrico 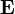y el campo magnético 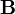vienen dados en términos de la densidad de carga 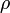y la densidad de corriente 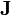como:

(1)

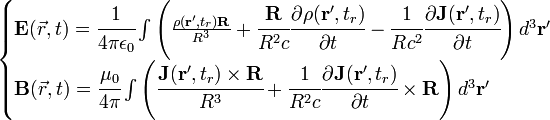
Donde 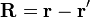, y 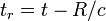. El uso del tiempo retardado signifca que el campo en el instante t a una distancia R de las cargas depende de como estaban las cargas situadas en un instante anterior, debido a la velocidad de propagación finita del campo el campo creado por las cargas ahora, se manifiesta sólo en tiempos avanzados a grandes distancias, por lo que no existe una conexión entre la posición de las cargas "ahora" y el campo medido "ahora" a grandes distancias de las cargas.

Campo magnético en presencia de medios dieléctricos y diamagnéticos

Las dos expresiones anteriores para el campo eléctrico y magnético admiten extensiones al caso de campos electromagnéticos en medios dieléctricos arbitrarios.^[1]

Los campos macroscópicos 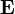, , 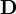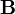y 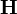se expresan entonces en términos de la densidad de carga 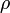, la densidad de corriente 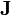, la polarización 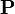, y la magnetización .

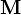Discusión

Referencia