El efecto Sunyaev-Zeldovich (efecto SZ) es el resultado de la interacción de la radiación de fondo, con electrones libres a una temperatura mayor. Esta interacción se da en las grandes estructuras del universo como los supercúmulos o cúmulos galácticos. Teniendo como resultado neto un corrimiento al azul en el espectro del CMB.

Idea Física

La densidad electrónica N_e en un cúmulo galáctico a una temperatura entre 10⁷K y 10⁹K producen una dispersión en la radiación de fondo. El efecto neto de esta dispersión es, por un lado, la disminución de intensidad en el CMB antes de los 220GHz y un aumento en la intensidad registrada después de los 220GHz. Este efecto hace ver en algunos casos regiones del CMB más frías (150GHz), regiones homogéneas (220GHz) y regiones más calientes (275GHz). Si por ejemplo, hacemos un censo a 275GHz de la radiación de fondo, observaremos regiones mucho más calientes que el promedio, descubriendo así las estructuras de los cúmulos galácticos, estas variaciones no tienen nada que ver con las fluctuaciones de densidad del CMB.

Calculando la Distancia a un Cumulo

Debido a que este fenómeno es independiente del corrimiento al rojo, podemos calcular la distancia a la que se encuentra el cumulo a partir del efecto S-Z y la emisión en rayos X producido por el bremstrahlung.

Si suponemos que el cumulo es esférico y esta a una distancia D, con un diámetro angular y con un diámetro L, entonces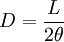

el ángulo θ lo podemos sacar del efecto S-Z, para obtener L usamos lo siguiente.

Sabemos que la emisión bremstrahlung en rayos X es

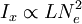
Y por el efecto S-Z que

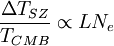donde ΔT_SZ es la diferencia de temperatura producida por el efecto S-Z, T_CMB es la temperatura del CMB, L el diámetro del cumulo y N_e la densidad electrónica,

entonces:

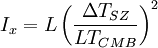
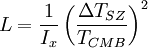
así, la distancia es:

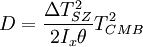
este método es independiente del corrimiento al rojo, dando un parámetro más, para encontrar la constante de Hubble.