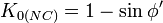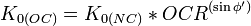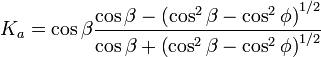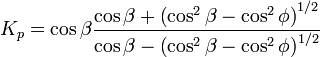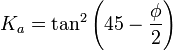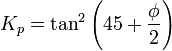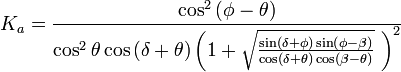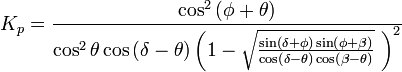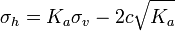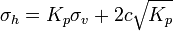Presión lateral del suelo

Presión lateral del suelo

Presión lateral del suelo

Un ejemplo de los principios de presión horizontal: un muro de contención de tierras

Presión lateral del suelo es la presión que el suelo ejerce en el plano horizontal. Las aplicaciones más comunes de la teoría de presiones laterales en suelos son el diseño de estructuras cimentadas como muros de tierras, zapatas, túneles y para determinar la fricción del terreno en la superficie de cimentaciones profundas. Para describir la presión que un suelo puede ejercer se usa un coeficiente de presión lateral, K. K es el ratio de presión lateral u horizontal respecto a la presión vertical (K = σh'/σv'). Esta fórmula está asumida por ser directamente proporcional y se cumple en cualquier punto del suelo. K puede depender de las propiedades mecánicas del suelo y de la historia tensional del suelo. Los coeficientes de presión lateral puede variar dentro de tres categorías: presión en reposo, presión activa y presión pasiva.

Los coeficientes de presión son usados en análisis de ingeniería geológica dependiendo de las características de su aplicación. Existen muchas teoría para predecir la presión lateral, algunas empíricas y otras analíticas.

Contenido

Presión en reposo

La presión en reposo, representadas por K0, es la presión horizontal del terreno. Esta puede ser medida directamente por el test dilatométrico (DMT) o por un "borehole pressuremter test" (PMT). Estos experimentos son caros, por eso se usan relaciones empíricas para predecir el resto de presiones que son más difíciles de obtener y que dependen generalmente del ángulo de rozamiento interno. Algunas fórmulas son:

Jaky (1948)[1] para suelos normalmente consolidados:

K_{0(NC)} = 1 - \sin \phi ' \

Mayne & Kulhawy (1982)[2] para suelos sobreconsolidados:

K_{0(OC)} = K_{0(NC)} * OCR^{(\sin \phi ')} \

La última requiere un perfil OCR profundo para ser determinada.

Presión activa y pasiva

Diferentes muros de contención diseñados para aguantar distintos empujes.

El estado activo ocurre cuando existe una relajación en la masa de suelo que lo permite moverse hacia fuera del espacio que limitaba la tensión del suelo (por ejemplo un muro de tierra que se rompe); esto es que el suelo está fallando por extenderse. Ésta es la presión mínima a la que el suelo puede ser sometida para que no se rompa. Al contrario el estado pasivo ocurre cuando la masa de suelo está sometida a una fuerza externa que lleva al suelo a la tensión limite de confinamiento. Esta es la máxima presión a la que puede ser sometida un suelo en el plano horizontal.

Teoría de Rankine

La teoría de Rankine, desarrollada en 1857,[3] es la solución a un campo de tensiones que predice las presiones activas y pasivas del terreno. Esta solución asume que el suelo está cohesionado, tiene un pared que está friccionando, la superficie suelo-pared es vertical, el plano de rotura en este caso sería planar y la fuerza resultante es paralela a la superficie libre del talud. Las ecuaciones de los coeficientes para presiones activas y pasivas aparecen a continuación. Observe que φ' es el ángulo de rozamiento del suelo y la inclinación del talud respecto a la horizontal es el ángulo β.

K_a = \cos\beta \frac{\cos \beta - \left(\cos ^2 \beta - \cos ^2 \phi \right)^{1/2}}{\cos \beta + \left(\cos ^2 \beta - \cos ^2 \phi \right)^{1/2}}
K_p = \cos\beta \frac{\cos \beta + \left(\cos ^2 \beta - \cos ^2 \phi \right)^{1/2}}{\cos \beta - \left(\cos ^2 \beta - \cos ^2 \phi \right)^{1/2}}

Para el caso en que β sea 0, las ecuaciones de arriba se simplifican como:

K_a = \tan ^2 \left( 45 - \frac{\phi}{2} \right) \
K_p = \tan ^2 \left( 45 + \frac{\phi}{2} \right) \

Teoría de Coulomb

Coulomb (1776)[4] fue el primero en estudiar el problema de las presiones laterales del terreno y estructuras de retención. Coulomb se limitó a usar la teoría de equilibrio que considera que un bloque de terreno en rotura como un cuerpo libre (o sea en movimiento) para determinar la presión lateral limitante. La presión limitante horizontal en fallo en extensión o compresión se determinan a partir de Ka y Kp respectivamente.

K_a = \frac{ \cos ^2 \left( \phi - \theta \right)}{\cos ^2 \theta \cos \left( \delta + \theta \right) \left( 1 + \sqrt{ \frac{ \sin \left( \delta + \phi \right) \sin \left( \phi - \beta \right)}{\cos \left( \delta + \theta \right) \cos \left( \beta - \theta \right)}} \ \right) ^2}
K_p = \frac{ \cos ^2 \left( \phi + \theta \right)}{\cos ^2 \theta \cos \left( \delta - \theta \right) \left( 1 - \sqrt{ \frac{ \sin \left( \delta + \phi \right) \sin \left( \phi + \beta \right)}{\cos \left( \delta - \theta \right) \cos \left( \beta - \theta \right)}} \ \right) ^2}

Relación de Bell

Para suelos con cohesión Bell desarrolló una solución analítica que usa la raíz del coeficiente K para predecir la contribución de la cohesión a la presión resultante. Estas ecuaciones expresan las presiones horizontales totales. El primer término representa la contribución no cohesiva y el segundo término la contribución cohesiva. La primera ecuación es para una situación activa y la segunda para una situación pasiva:

\sigma_h = K_a \sigma_v - 2c \sqrt{K_a} \
\sigma_h = K_p \sigma_v + 2c \sqrt{K_p} \

Véase también

Referencias

  • Coduto, Donald (2001), Foundation Design, Prentice-Hall, ISBN 0-13-589706-8

Notas

  1. ↑ Jaky J. (1948) Pressure in soils, 2nd ICSMFE, London, Vol. 1, pp 103-107.
  2. ↑ Mayne, P.W. and Kulhawy, F.H. (1982). “K0-OCR relationships in soil”. Journal of Geotechnical Engineering, Vol. 108 (GT6), 851-872.
  3. ↑ Rankine, W. (1857) On the stability of loose earth. Philosophical Transactions of the Royal Society of London, Vol. 147.
  4. ↑ Coulomb C.A., (1776). Essai sur une application des regles des maximis et minimis a quelques problemes de statique relatifs a l'architecture. Memoires de l'Academie Royale pres Divers Savants, Vol. 7
Obtenido de "Presi%C3%B3n lateral del suelo"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Suelo (ingeniería) — Para otros usos de este término, véase Suelo (desambiguación). Desde el punto de vista de la ingeniería, suelo es el sustrato físico sobre el que se realizan las obras, del que importan las propiedades físico químicas, especialmente las… …   Wikipedia Español

  • San Vicente del Raspeig — Saltar a navegación, búsqueda San Vicente del Raspeig / Sant Vicent del Raspeig San Vicente del Raspeig …   Wikipedia Español

  • Ciudad del Carmen — Para otros usos de este término, véase Carmen. Ciudad del Carmen Escudo …   Wikipedia Español

  • Reglas del fútbol — Saltar a navegación, búsqueda Las reglas del fútbol, también conocidas como las reglas de juego a nivel de la FIFA, son las reglas que rigen el fútbol en todo el mundo. Los cambios en las mismas están a cargo de la International Football… …   Wikipedia Español

  • Historia del Club Atlético de Madrid — El Club Atlético de Madrid es un club de fútbol español, de la ciudad de Madrid. Fue fundado el 26 de abril de 1903 y en la actualidad juega en la Primera División de España. El club ejerce de local en el Estadio Vicente Calderón, recinto ubicado …   Wikipedia Español

  • Cimentación — Venecia es quizás uno de los ejemplos más notables de la cimentación por medio de pilotes de madera. Se denomina cimentación al conjunto de elementos estructurales cuya misión es transmitir las cargas de la edificación o elementos apoyados a este …   Wikipedia Español

  • Erupción del Monte Santa Helena en 1980 — Saltar a navegación, búsqueda …   Wikipedia Español

  • Pilote (cimentación) — Saltar a navegación, búsqueda Hincado de pilotes en la modernización de vías férreas en Chojnów, Polonia. Se denomina pilote a un elemento constructivo utilizado para cimentación de obras, que permite trasladar las cargas hasta un estrato… …   Wikipedia Español

  • Muro de contención — construido en piedra. Se denomina muro de contención a un tipo estructura de contención rígida, destinada a contener algún material, generalmente tierras. Contenido 1 …   Wikipedia Español

  • Orden del Císter — Nombre latino Ordo Cisterciensis Siglas O. Cist. Nombre común …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”