- Energía gravitatoria
-
Energía gravitatoria
La energía potencial se debe a la posición respecto a la del suelo tomado como referencia. Si estas en pie en un trampolín de tres metros de altura, tienes 3 veces mas energía que en el trampolín de 1 metro. La energía potencial que depende de la altura se llama Energía Potencial Gravitatoria. El peso determina también la cantidad de Epg que tiene un objeto. El dicho “Cuanto más grandes son, con más ruido caen” es una referencia al efecto del peso en la energía gravitacional. Tienes mucha mas Epg si cargas una mochila pesada que si cargas una liviana.
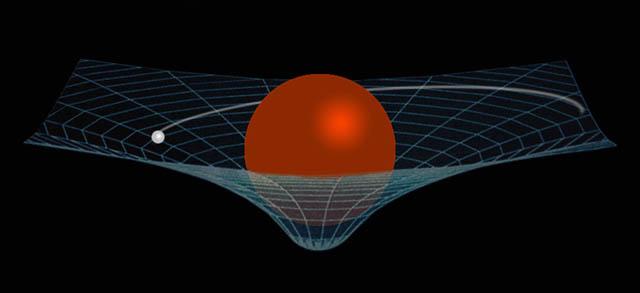 La gravedad
La gravedad
La relación entre Epg, peso y altura, puede expresarse con la siguiente fórmula: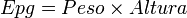
Según esta fórmula, cuanto mayor es el peso, mayor es la Epg. Cuanto mayor es la altura sobre una superficie, mayor es la energía potencial gravitacional.
La energía potencial es la capacidad que tienen los cuerpos para realizar un trabajo (\ W), dependiendo de la configuración que tengan en un sistema de cuerpos que ejercen fuerzas entre sí. Puede pensarse como la energía almacenada en un sistema, o como una medida del trabajo que un sistema puede entregar. Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.Energía potencial gravitatoria La fuerza gravitatoria mantiene a los planetas en órbita en torno al sol
Este tipo de energía está asociada con el grado de separación entre dos cuerpos, los cuales se atraen mediante fuerza gravitacional.
- Caso general. La energía potencial gravitatoria VG de una partícula material de masa m situada dentro del campo gravitatorio terrestre viene dada por:
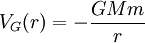
Donde:
 : distancia entre la partícula material del centro de la Tierra (es decir, su altura).
: distancia entre la partícula material del centro de la Tierra (es decir, su altura).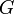 : constante de gravitación universal.
: constante de gravitación universal.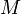 : masa de la tierra.
: masa de la tierra.
Esta última es la fórmula que necesitamos emplear, por ejemplo, para estudiar el movimiento de satélites y misiles balísticos
- Cálculo simplificado. Cuando la distancia recorrida por un móvil h es pequeña, lo que sucede en la mayoría de las aplicaciones usuales (tiro parabólico, saltos de agua, etc.), podemos usar el desarrollo de Taylor a la anterior ecuación. Así si llamamos ir a la distancia al centro de la tierra, R al radio de la Tierra y h a la altura sobre la superficie de la Tierra tenemos:
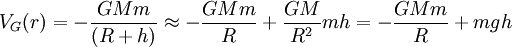
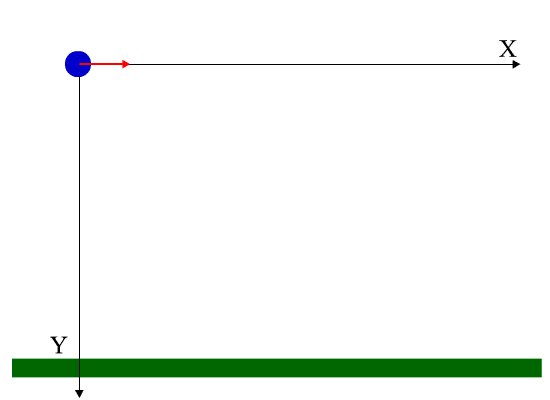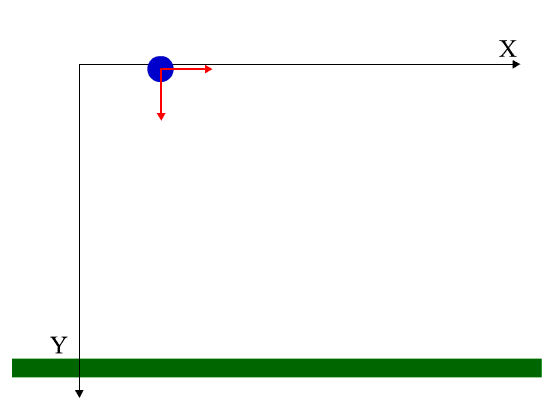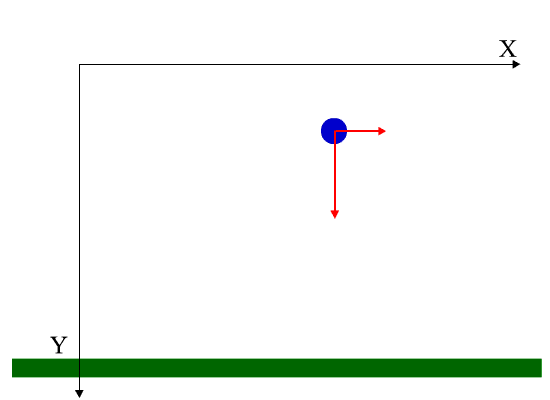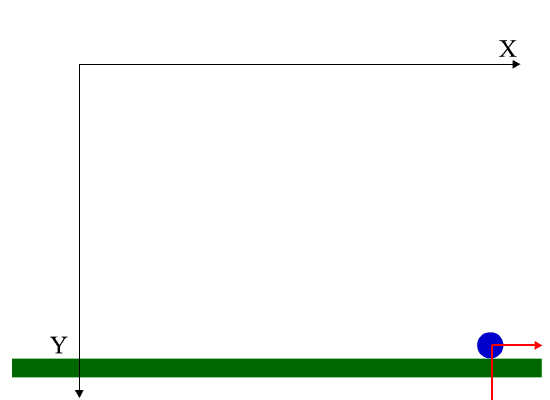 Tiro parabolico
Tiro parabolico
Donde hemos introducido la aceleración sobre la superfice: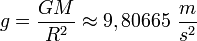
Por tanto la variación de la energía potencial gravitatoria al desplazarse un cuerpo de masa m desde una altura h1 hasta una altura h2 es:
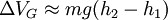
Dado que la energía potencial se anula cuando la distancia es infinita, frecuentemente se asigna energía potencial cero a la altura correspondiente a la del suelo, ya que lo que es de interés no es el valor absoluto de V, sino su variación durante el movimiento.Así, si la altura del suelo es h1 = 0, entonces la energía potencial a una altura h2 = h será simplemente VG = mgh.
Le podemos llamar así, aunque lo correcto sería fuerza. Es una de las 4 fundamentales del universo y es la encargada de que exista la gravedad. Todos los cuerpos interactúan gravitatoriamente con todos los demás cuerpos del universo, es sólo que la fuerza es despreciable por las distancias que los separan. Las partículas específicas se llaman gravitones (teóricamente, no se ha comprobado que existan).
Energía: La magnitud denominada energía enlaza todas las ramas de la física. En el ámbito de la mecánica, debe suministrarse energía para realizar trabajo; el trabajo se define como el producto de la fuerza por la distancia que recorre un objeto en la dirección de la fuerza. Cuando se ejerce una fuerza sobre un objeto pero la fuerza no hace que el objeto se mueva, no se realiza trabajo. La energía y el trabajo se expresan en las mismas unidades, como por ejemplo julios o ergios.
Referencias
- 1. ↑ «Space Solar Power Satellite Technology Development at the Glenn Research Center—An Overview» (en inglés) (2000) Consultado el viernes 21 de octubre del 2009
- 2. ↑ «Inclusión del Concepto de Masa Gravitacional Aparente en la Relatividad Especial» Consultado el sabado 31 de octubre del 2009
- 3. ↑ «Trabajo, energía y potencia versión PDF (en español)» Consultado el sabado 31 de octubre del 2009
- 4. ↑ «Yahoo respuestas» Consultado el sabado 30 de octubre del 2009
- 5. ↑ «Colegio Anglo Mexicano De Coyoacan versión PDF (en español)»
Véase también
- Energía
- Energía potencial
- Portal:Energía
Wikimedia foundation. 2010.
