El Ensayo sobre el principio de población es una obra del siglo XIX, publicado originalmente en inglés como An Essay on the Principle of Population (1798), es una obra de demografía escrita por el economista inglés Thomas Robert Malthus, en la que desarrolla la influyente teoría de que la población crece más rápidamente que los recursos, conduciendo a una progresiva pauperización de la población.

La predicción principal de dicha obra se conoce como ley de Malthus, que no se llegó a producir nunca debido a que ocurrió un fenómeno hoy conocido como transición demográfica.

Ley de Malthus

El trabajo de Malthus pretendía interpretar la desigualdad económica, la miseria y la pobreza de las masas trabajadoras bajo el capitalismo como una consecuencia práctica del crecimiento de la población y la escasez de recursos.

Malthus afirmaba que la población se duplicaba en cada 25 años, es decir, crecía en progresión geométrica, es decir, preenta un crecimiento exponencial), para ello se basó en los datos de crecimiento de población en Estados Unidos durante el siglo XVIII. Por otra parte Malthus supuso que los medios de subsistencia, en le mejor de los casos, aumentan en progresión aritmética, es decir, presentan un crecimiento lineal.

Su método positivo habla de buscar el camino del equilibrio mediante la muerte, con sus diferentes formas de alcanzarla como son las epidemias, el hambre y las guerras. Para Malthus, el alimento más barato debía ser el pan, pues sacia el apetito sin aportar demasiados nutrientes al organismo (de los marginados).

Así, Malthus pretendía que los proletarios construyesen sus viviendas en los terrenos pantanosos e insalubres, viendo con malos ojos a los individuos compasivos que creen hacerle un gran beneficio a la humanidad estudiando la manera de extirpar para siempre ciertas enfermedades.

Malthus cree que la miseria es una ley natural e inconmovible, contra la cual es inútil actuar. Por el contrario, si no bastan los cataclismos de la naturaleza, el Estado debe "contribuir" poniendo su ingrediente de guerras, desentendiéndose de la sanidad pública y de cualquier norma de protección humana. De ahí que se oponga a las llamadas "poor laws" (leyes de pobreza), estableciendo que los subsidios a los pobres no pueden impedir ni la pobreza ni el hambre: "Si los alimentos no alcanzan para todos, un subsidio a los pobres no puede aumentar su volumen, ya que lo único que puede traer consigo es el aumento de la cantidad de pobres, pero en ningún caso más riquezas."

Además, este libro le dio la idea de la selección natural a Charles Robert Darwin, que después de leerlo resolvió el enigma de la evolución. Dedujo que las poblaciones al final lucharían por los recursos y sólo sobrevivirían los más fuertes.

La teoría de Malthus sobre el crecimiento de la población:

También está relacionado con la ecuación de crecimiento logístico.

Modelo matemático

La ley de Malthus predecía por tanto la ocurrencia en el futuro de un fenómeno llamado castástrofe malthusiana en el que los recursos alimentarios serían claramente insostenibles para mantener a la población mundial y sobrevendrían graves guerras y hambrunas que diezmarían a la humanidad. Esta sección formaliza las ideas de Malthus en forma de ecuaciones diferenciales y calcula en función de ciertos parámetros el tiempo de ocurrencia de la catástrofe malthusiana en donde la cantidad de alimentos disponibles no es suficiente para sostener a toda la población.

Expresado en ecuaciones diferenciales el argumento de Malthus es el siguiente: Si P(t) es la población en el año t que crecería exponencialmente (progresión geométrica) y A(t) la cantidad total de alimentos que crecería linealmente (progresión aritmética) las tasas de aumento serían:

(1)

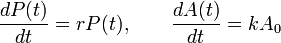
La solución de las dos ecuaciones anteriores lleva a que la cantidad de alimento por persona viene dada por:

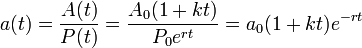
Doinde P₀ es la población inicial y A₀ es la dotación inicial de alimentos. Supongamos ahora que la cantidad mínima de alimentos o ingesta mínima por persona es a_min, entonces si las hipótesis de Malthus hubieran sido correctas para todo instante del tiempo, la cantidad de alimentos por persona se habría reducido hasta ser inferior a la cantidad mínima de alimentos por persona en el instante de la catástrofe malthusiana t_cm:

(2)

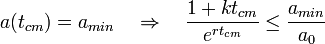
Puede verse que para cualesquiera valores positivos de r, k, A₀, P₀ y a_min existe un instante del tiempo dado por t_cm en el que se produce indefectiblemente la catástrofe malthusiana, si las ecuaciones de evolución (1) no cambian en todo el proceso. La solución de (2) viene dada mediante la función W de Lambert:

(3)

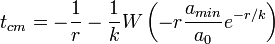
Fracaso y éxito de la ley de Malthus

Si bien en su momento muchas personas tomaron seriamente las predicciones de Malthus sobre las consecuencias del aumento de población, el pronóstico catastrofista no se cumplió por varias razones:

• En primer lugar ocurrió la llamada transición demográfica por la cual muchas sociedades a partir de un nivel de renta moderaron la tasa de natalidad, pasando de un crecimiento exponencial a un crecimiento logístico.
• Por otra parte la tasa de aumento de los recursos alimentarios ha crecido más rápido de lo previsto.

Esas dos hipótesis en conjunto sirven hacen que no se de la catástrofe malthusiana tras un tiempo finito como indica (3) ya que las relaciones de incremento de población e incremento de recursos reales han diferido de las previstas por Malthus.

Sin embargo, algunos autores como Jared Diamond al analizar el genocidio de Ruanda en su libro Colapso: por qué unas sociedades perduran y otras desaparecen, sugiere que los datos de aumento de población y extrema partición de la tierra, sentaron probabilísticamente la base de un conflicto malthusiano en el que el deterioro de las condiciones de vida, facilitó la difusión de actitudes genocidas.

Referencia

Bibliografía

• Diamond, Jared (2005), Collapse: How Societies Choose to Fail or Succeed, ISBN 0-14-303655-6. (edición inglesa)

Enlaces externos

• Malthus, el economista

Véase también

• Alimentación humana