Entropía de Shannon

Entropía de Shannon

Entropía de Shannon

La entropía definida por Shannon, referida a la teoría de la información, hace referencia a la cantidad media de información que contiene una variable aleatoria o, en particular, una fuente transmisión binaria.

La información que aporta un determinado valor, 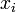x_i \,\!, de una variable aleatoria discreta 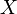X \,\! se define como: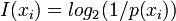

I(x_i) = log_2( 1 / p(x_i) ) \,\!

cuya unidad es el bit se utiliza el logaritmo en base 2 (por ejemplo, cuando se emplea el logaritmo neperiamo se habla de nats).

La entropía o información media de la variable aleatoria discreta, 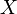X \,\!, se determina como la información media del conjunto de valores discretos que puede adoptar (también medida en bits):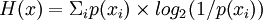

H(x) = \Sigma_i p(x_i)\times log_2( 1/p(x_i)) \,\!

Además de su definición y estudio, Shannon demostró analíticamente que la entropía es el límite máximo al que se puede comprimir una fuente sin ninguna pérdida de información.


Enlaces de Interés

Significado y origen de la fórmula de Shannon en serie de artículos sobre televisión digital Excelente

Obtenido de "Entrop%C3%ADa de Shannon"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Entropía (información) — Saltar a navegación, búsqueda Para otros usos de este término, véase Entropía. Entropía es un concepto en termodinámica, mecánica estadística y teoría de la información. Los conceptos de información y entropía están ampliamente relacionados entre …   Wikipedia Español

  • Entropía de Kolmogórov — Saltar a navegación, búsqueda La entropía de Kolmogórov se define como principio que mide la pérdida de información a lo largo de la evolución del sistema. También es definida como la suma de exponentes de Liapunov. Tiene una gran importancia, en …   Wikipedia Español

  • Nat (información) — Un nat (también denominado nit o nepit) es una unidad logarítmica de información o entropía, basada en logaritmos naturales o neperianos (con base e), en vez de en logaritmos binarios (con base 2) utilizados cuando la información se mide en bits …   Wikipedia Español

  • Alfréd Rényi — (20 de marzo de 1921 – 1 de febrero de 1970) fue un matemático húngaro que hizo importantes contribuciones a la teoría de combinatoria y de teoría de grafos sobre grafos aleatorios.[1] [2] …   Wikipedia Español

  • Conversión analógica-digital — La conversión analógica digital (CAD) consiste en la transcripción de señales analógicas en señales digitales, con el propósito de facilitar su procesamiento (codificación, compresión, etc.) y hacer la señal resultante (la digital) más inmune al… …   Wikipedia Español

  • Índice de Theil — El índice de Theil es una medida de desigualdad basada en la entropía de Shannon. Sirve para medir y comparar la distribución de la renta. Según Cotler, Pablo dicho índice permite ser desagregado en un componente de desigualdad al interior de los …   Wikipedia Español

  • Teoría de la información — Este artículo está siendo desarrollado y forma parte de un proyecto educativo. Es posible que a causa de ello haya lagunas de contenido o deficiencias de formato. Si quieres puedes ayudar y editar, pero por favor antes de realizar correcciones… …   Wikipedia Español

  • Libreta de un solo uso — Extracto de una libreta de un solo uso. En criptografía, la libreta de un solo uso (del inglés one time pad) es un algoritmo de cifrado por el que el texto en claro se combina con una clave aleatoria o «libreta» igual de larga que el texto en… …   Wikipedia Español

  • Codificación Huffman — Árbol de Huffman generado para las frecuencias de apariciones exactas del texto Esto es un ejemplo de árbol de Huffman . las frecuencias y códigos de cada carácter se muestran abajo. Codificar esta frase usando este código requiere 156 bits, sin… …   Wikipedia Español

  • Capacidad de canal — Saltar a navegación, búsqueda En Teoría de la Información, la capacidad de un canal de comunicación es la cantidad máxima de información que puede transportar dicho canal de forma fiable, es decir, con una probabilidad de error tan pequeña como… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”