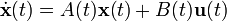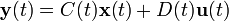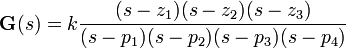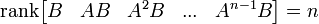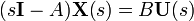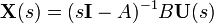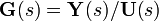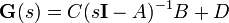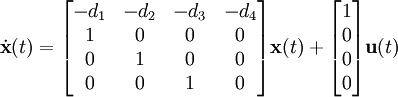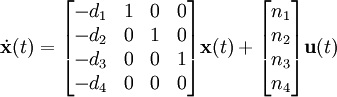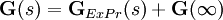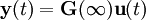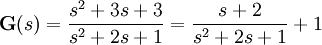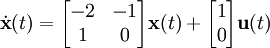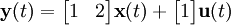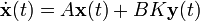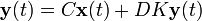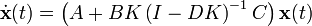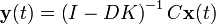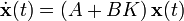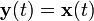Espacio de estados

Saltar a navegación, búsqueda

En ingeniería de control, una representación de espacios de estados es un modelo matemático de un sistema físico descrito mediante un conjunto de entradas, salidas y variables de estado relacionadas por ecuaciones diferenciales de primer orden que se combinan en una ecuación diferencial matricial de primer orden. Para prescindir del número de entradas, salidas y estados, las variables son expresadas como vectores y las ecuaciones algebraicas se escriben en forma matricial (esto último sólo puede hacerse cuando el sistema dinámico es lineal e invariante en el tiempo). La representación de espacios de estado (también conocida como aproximación en el dominio del tiempo) provee un modo compacto y conveniente de modelar y analizar sistemas con múltiples entradas y salidas. Con $p$ entradas y $q$ salidas, tendríamos que escribir 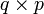$q \times p$ veces la transformada de Laplace para procesar toda la información del sistema. A diferencia de la aproximación en el dominio de la frecuencia, el uso de la representación de espacios de estado no está limitada a sistemas con componentes lineales ni con condiciones iniciales iguales a cero. El espacio de estado se refiere al espacio de $n$ dimensiones cuyos ejes coordenados están formados por variables de estados. El estado del sistema puede ser representado como un vector dentro de ese espacio.

Variables de estado

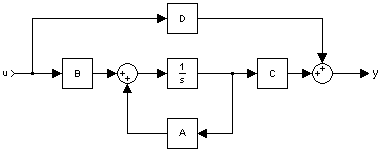Modelo de espacios de estado típico

Artículo principal: Variable de estado (sistema dinámico)

Las 'variables de estado son el conjunto más pequeño de variables que pueden representar al sistema dinámico completo en un tiempo cualquiera. Las variables de estado deben ser linealmente independientes; una variable de estado no puede ser una combinación lineal de otras variables de estado. El número mínimo de variables de estado necesarias para representar un sistema dado es $n$ , es normalmente igual al orden de la ecuación diferencial que define al sistema. Si el sistema es representado en forma de función de transferencia, el número mínimo de variables de estado es igual al orden del denominador de la función transferencia después de haber sido reducido a una fracción propia. Cabe destacar que al convertir una representación de espacios de estados a una forma de función transferencia podría perderse alguna información interna sobre el sistema, indicando que dicho sistema es estable, cuando la representación de espacios de estados indica que es inestable en ciertos puntos. En circuitos eléctricos, el número de variables de estados es a menudo, pero no siempre, igual al número de elementos que almacenan energía en los circuitos, como capacitores e inductores.

Sistemas lineales

Una forma general de representación de espacios de estado de un sistema linear con $p$ entradas, $q$ salidas y $n$ variables de estado se escribe de la siguiente forma:

$\dot{\mathbf{x}}(t) = A(t) \mathbf{x}(t) + B(t) \mathbf{u}(t)$

$\mathbf{y}(t) = C(t) \mathbf{x}(t) + D(t) \mathbf{u}(t)$

donde

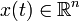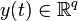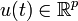$x(t) \in \mathbb{R}^n$ ; $y(t) \in \mathbb{R}^q$ ; $u(t) \in \mathbb{R}^p$ ;

$\operatorname{dim}[A(\cdot)] = n \times n$ ,

$\operatorname{dim}[B(\cdot)] = n \times p$ ,

$\operatorname{dim}[C(\cdot)] = q \times n$ ,

$\operatorname{dim}[D(\cdot)] = q \times p$ ,

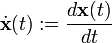$\dot{\mathbf{x}}(t) := {d\mathbf{x}(t) \over dt}$ .

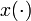$x(\cdot)$ es llamado vector de estados, 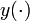$y(\cdot)$ es llamado vector de salida, 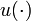$u(\cdot)$ es llamado vector de entradas (o control), 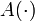$A(\cdot)$ es la matriz de estados, 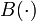$B(\cdot)$ es la matriz de entrada, 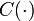$C(\cdot)$ es la matriz de salida, y 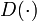$D(\cdot)$ es la matriz de transmisión directa. Por simplicidad, 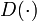$D(\cdot)$ normalmente se toma como la matriz cero, p. ej.: se elije que el sistema no tenga transmisión. Nótese que en esta formulación general se supone que todas las matrices son variantes en el tiempo, p. ej.: algunos o todos sus elementos pueden depender del tiempo. La variable temporal $t$ puede ser una "contínua" (p. ej.: 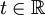$t \in \mathbb{R}$ ) o una discreta (p. ej.: 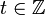$t \in \mathbb{Z}$ ): en éste último caso la variable temporal es generalmente indicada como $k$ . Dependiendo de las consideraciones tomadas, la representación del modelo de espacios de estado puede tomar las siguientes formas:

Tipo de sistema	Modelo de espacio de estados
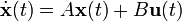
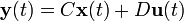
Contínuo e invariante en el tiempo	$\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)$ $\mathbf{y}(t) = C \mathbf{x}(t) + D \mathbf{u}(t)$
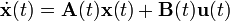
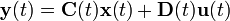
Contínuo y variante en el tiempo	$\dot{\mathbf{x}}(t) = \mathbf{A}(t) \mathbf{x}(t) + \mathbf{B}(t) \mathbf{u}(t)$ $\mathbf{y}(t) = \mathbf{C}(t) \mathbf{x}(t) + \mathbf{D}(t) \mathbf{u}(t)$
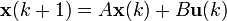
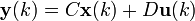
Discreto e invariante en el tiempo	$\mathbf{x}(k+1) = A \mathbf{x}(k) + B \mathbf{u}(k)$ $\mathbf{y}(k) = C \mathbf{x}(k) + D \mathbf{u}(k)$
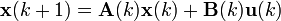
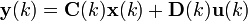
Discreto y variante en el tiempo	$\mathbf{x}(k+1) = \mathbf{A}(k) \mathbf{x}(k) + \mathbf{B}(k) \mathbf{u}(k)$ $\mathbf{y}(k) = \mathbf{C}(k) \mathbf{x}(k) + \mathbf{D}(k) \mathbf{u}(k)$
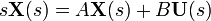
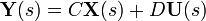
Transformada de Laplace de contínua e invariante en el tiempo	$s \mathbf{X}(s) = A \mathbf{X}(s) + B \mathbf{U}(s)$ $\mathbf{Y}(s) = C \mathbf{X}(s) + D \mathbf{U}(s)$
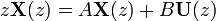
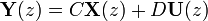
Transformada Z de discreta e invariante en el tiempo	$z \mathbf{X}(z) = A \mathbf{X}(z) + B \mathbf{U}(z)$ $\mathbf{Y}(z) = C \mathbf{X}(z) + D \mathbf{U}(z)$

La estabilidad y la respuesta natural característica de un sistema puede ser estudiado mediante los eigen-valores (o valores propios) de la matriz $A$ . La estabilidad de un modelo de espacio de estados invariante en el tiempo puede ser fácilmente determinado observando la función transferencia del sistema en forma factorizada. Tendría un forma parecida a la siguiente:

$\textbf{G}(s) = k \frac{ (s - z_{1})(s - z_{2})(s - z_{3}) }{ (s - p_{1})(s - p_{2})(s - p_{3})(s - p_{4}) }$

El denominador de la función transferencia es igual al polinomio característico encontrado tomando el determinante de $s I - A$ ,

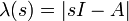$\mathbf{\lambda}(s) = |sI - A|$ .

Las raíces de este polinomio (los eigen-valores) proporcionan los polos en la función transferencia del sistema. Dichos polos pueden ser utilizados para analizar si el sistema es asintótica o marginalmente estable. Otra alternativa para determinar la estabilidad, en la cual no involucra los cálculos de los eigen-valores, es analizar la estabilidad de Liapunov del sistema. Los ceros encontrados en el numerador de 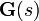$\textbf{G}(s)$ puede usarse de manera similar para determinar si el sistema posee una fase mínima.

El sistema podría ser estable con respecto a sus entradas y salidas aún si es internamente inestable. Este pordría ser el caso si polos inestables son cancelados por ceros.

Controlabilidad

Artículo principal: Controlabilidad

La condición de controlabilidad de estados implica que es posible, mediante entradas admisibles, dirigir los estados desde cualquier valor inicial a cualquier valor final dentro de un intervalo de tiempo. Un modelo de espacio de estados contínuo e invariante en el tiempo es controlable si y sólo si

$\operatorname{rank}\begin{bmatrix}B& AB& A^{2}B& ...& A^{n-1}B\end{bmatrix} = n$

Observabilidad

Artículo principal: Observabilidad

La observabilidad es la medida de que tan bien los estados internos de un sistema pueden ser inferidos conociendo las salidas externas. La observadlidad y la controlabilidad son matemáticamente duales.

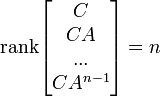
Un modelo de espacio de estados contínuo e invariante en el tiempo es observable si y sólo si:

$\operatorname{rank}\begin{bmatrix}C\\ CA\\ ...\\ CA^{n-1}\end{bmatrix} = n$

(el rango de una matriz es el número de filas linealmente independientes.)

Función de transferencia

Artículo principal: Función de transferencia

La función de transferencia de un modelo de espacio de estados contínuo e invariante en el tiempo puede ser obtenida de la siguiente manera:

Tomando la transformada de Laplace de

$\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)$

tenemos que

$s\mathbf{X}(s) = A \mathbf{X}(s) + B \mathbf{U}(s)$

Luego, dividimos entre 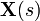$\mathbf{X}(s)$ , dando

$(s\mathbf{I} - A)\mathbf{X}(s) = B\mathbf{U}(s)$

$\mathbf{X}(s) = (s\mathbf{I} - A)^{-1}B\mathbf{U}(s)$

esto es sustituido por 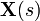$\mathbf{X}(s)$ en la ecuación de salida

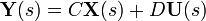$\mathbf{Y}(s) = C\mathbf{X}(s) + D\mathbf{U}(s)$ , nos queda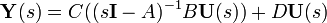

$\mathbf{Y}(s) = C((s\mathbf{I} - A)^{-1}B\mathbf{U}(s)) + D\mathbf{U}(s)$

Como la función de transferencia está definida como la tasa de salida sobre la entrada de un sistema, tomamos

$\mathbf{G}(s) = \mathbf{Y}(s) / \mathbf{U}(s)$

y sustituimos las expresiones previas por 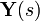$\mathbf{Y}(s)$ con respecto a 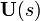$\mathbf{U}(s)$ , quedando

$\mathbf{G}(s) = C(s\mathbf{I} - A)^{-1}B + D$

Claramente 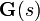$\mathbf{G}(s)$ debe tener $q$ por $p$ dimensiones, así como un total de $q p$ elementos. Entonces para cada entrada hay $q$ funciones de transferencias con uno por cada salida. Esta es la razón por la cual la representación de espacios de estados puede fácilmente ser la elección preferida para sistemas de múltiples entradas, múltiples salidas (MIMO, por sus siglas en inglés: Multiple-Input, Multiple-Output).

Formas canónicas

Cualquier función transferencia que es estrictamente propia puede ser escrita como un espacio de estados con la siguiente aproximación:

Dada una función transferencia, expandirla para revelar todos los coeficientes en el numerador y en el denominador. Resultando en la siguiente forma:

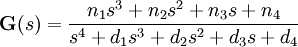$\textbf{G}(s) = \frac{n_{1}s^{3} + n_{2}s^{2} + n_{3}s + n_{4}}{s^{4} + d_{1}s^{3} + d_{2}s^{2} + d_{3}s + d_{4}}$ .

Los coeficientes pueden ser ahora insertados directamente en el modelo de espacio de estados mediante la siguiente aproximación:

$\dot{\textbf{x}}(t) = \begin{bmatrix} -d_{1}& -d_{2}& -d_{3}& -d_{4}\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0 \end{bmatrix}\textbf{x}(t) + \begin{bmatrix} 1\\ 0\\ 0\\ 0\\ \end{bmatrix}\textbf{u}(t)$

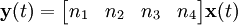$\textbf{y}(t) = \begin{bmatrix} n_{1}& n_{2}& n_{3}& n_{4} \end{bmatrix}\textbf{x}(t)$ .

Esta disposición de espacio de estados es llamada forma canónica controlable porque el modelo resultante garantiza que es controlable.

Los coeficientes de la función transferencia pueden ser usados también para construir otro tipo de forma canónica

$\dot{\textbf{x}}(t) = \begin{bmatrix} -d_{1}& 1& 0& 0\\ -d_{2}& 0& 1& 0\\ -d_{3}& 0& 0& 1\\ -d_{4}& 0& 0& 0 \end{bmatrix}\textbf{x}(t) + \begin{bmatrix} n_{1}\\ n_{2}\\ n_{3}\\ n_{4} \end{bmatrix}\textbf{u}(t)$

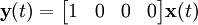$\textbf{y}(t) = \begin{bmatrix} 1& 0& 0& 0 \end{bmatrix}\textbf{x}(t)$ .

Esta disposición es llamada forma canónica observable porque el modelo resultante garantiza que es observable.

Funciones transferencia propias

Las funciones transferencia que son sólo propias (y no estrictamente propias) pueden también transformadas a las formas canónicas. El artificio utilizado es el de separar la función transferencia en dos partes, una estrictamente propia y una constante.

$\textbf{G}(s) = \textbf{G}_{ExPr}(s) + \textbf{G}(\infty)$

La función transferencia estrictamente propia puede ser ahora transformada a las representaciones de espacio de estados canónicas utilizando las técnicas mostradas anteriormente. La representación de espacio de estados de la constante es trivial.

$\textbf{y}(t) = \textbf{G}(\infty)\textbf{u}(t)$

Juntando ambos términos obtenemos las representaciones de espacio de estados con las matrices A, B y C determinadas por la parte estrictamente propia y la matriz D determinada por la constante.

Aquí un ejemplo para aclarar:

$\textbf{G}(s) = \frac{s^{2} + 3s + 3}{s^{2} + 2s + 1} = \frac{s + 2}{s^{2} + 2s + 1} + 1$

lo que conduce a la siguiente representación controlable

$\dot{\textbf{x}}(t) = \begin{bmatrix} -2& -1\\ 1& 0\\ \end{bmatrix}\textbf{x}(t) + \begin{bmatrix} 1\\ 0\end{bmatrix}\textbf{u}(t)$

$\textbf{y}(t) = \begin{bmatrix} 1& 2\end{bmatrix}\textbf{x}(t) + \begin{bmatrix} 1\end{bmatrix}\textbf{u}(t)$

Nótese como la salida depende directamente de la entrada. Esto se debe a la constante 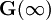$\textbf{G}(\infty)$ en la función transferencia.

Realimentación

Un método utilizado para realimentar es el de multiplicar la salida por una matriz K y colocar el resultado como la entrada del sistema: 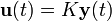$\mathbf{u}(t) = K \mathbf{y}(t)$ . Como los valores de K no están restrigidos y pueden cambiarse de signo para la realimentación negativa. La presencia de un signo negativo (la notación común) es únicamente con fines de notación y su ausencia no afecta los resultados.

$\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)$

$\mathbf{y}(t) = C \mathbf{x}(t) + D \mathbf{u}(t)$

resulta en

$\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B K \mathbf{y}(t)$

$\mathbf{y}(t) = C \mathbf{x}(t) + D K \mathbf{y}(t)$

resolviendo la ecuación de salida para 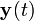$\mathbf{y}(t)$ y sustituyendo en la ecuación de estados resulta en

$\dot{\mathbf{x}}(t) = \left(A + B K \left(I - D K\right)^{-1} C \right) \mathbf{x}(t)$

$\mathbf{y}(t) = \left(I - D K\right)^{-1} C \mathbf{x}(t)$

La ventaja de esto es que los valores propios de A pueden ser controlados eligiendo K apropiadamente mediante la descomposición en sus valores propios de 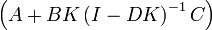$\left(A + B K \left(I - D K\right)^{-1} C \right)$ . Esto asume que el sistema de lazo abierto es controlable o que los valores propios inestables de A pueden estabilizarse mediante la elección apropiada de K.

Ua simplificación común de este sistema es eliminar D y elegir C igual a la unidad, lo que reduce las ecuaciones a

$\dot{\mathbf{x}}(t) = \left(A + B K \right) \mathbf{x}(t)$

$\mathbf{y}(t) = \mathbf{x}(t)$

Esto reduce la descomposición de los valores propios a sólo $A + B K$ .

Obtenido de "Espacio de estados"

Categoría: Ingeniería

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

Museo Nacional del Aire y el Espacio de Estados Unidos — Entrada del museo en el National Mall El Museo Nacional del Aire y el Espacio (National Air and Space Museum) de la Institución Smithsonian en los Estados Unidos contiene la mayor colección de aviones y naves espaciales del mundo. Además, es un… … Wikipedia Español
Espacio de Hilbert equipado — Saltar a navegación, búsqueda En matemáticas, un espacio de Hilbert equipado (EHE) es una generalización de los espacios de Hilbert que permite ligar la teoría de distribuciones y los aspectos cuadrado integrables del análisis funcional. Tales… … Wikipedia Español
Espacio fásico — de un sistema dinámico con estabilidad focal. En mecánica clásica, el espacio fásico, espacio de fases o diagrama de fases es una construcción matemática que permite representar el conjunto de posiciones y momentos conjugados de un sistema de… … Wikipedia Español
Espacio entre sofá y tele — Saltar a navegación, búsqueda El espacio entre el sofá y la tele ha estado desde siempre íntimamente ligado al espacio de la zona de estar comedor de la vivienda. Este espacio, a su vez, es la parte esencial de la vivienda, de forma que no se… … Wikipedia Español
Espacio de Fock — Saltar a navegación, búsqueda El espacio de Fock , en mecánica cuántica es un espacio de Hilbert especial, que se construye como suma directa de productos tensoriales de otro espacio de Hilbert dado . Este espacio se usa para describir el estado… … Wikipedia Español
Espacio exterior — Saltar a navegación, búsqueda Capas de la atmósfera (no a escala). El espacio exterior o espacio vacío, también simplemente llamado espacio, se refiere a las regiones relativamente vacías del universo fuera de las atmósferas de los cuerpos… … Wikipedia Español
Espacio de Hilbert — Saltar a navegación, búsqueda En matemáticas, el concepto de espacio de Hilbert es una generalización del concepto de espacio euclídeo. Esta generalización permite que nociones y técnicas algebraicas y geométricas aplicables a espacios de… … Wikipedia Español
Espacio geográfico — Saltar a navegación, búsqueda El espacio geográfico es un concepto utilizado por la ciencia geográfica para definir el espacio organizado por la sociedad. Es el espacio en el que se desenvuelven los grupos humanos en su interrelación con el medio … Wikipedia Español
Espacio (desambiguación) — Saltar a navegación, búsqueda Espacio es un concepto abstracto utilizado en matemática, física, filosofía, informática, y otras ciencias. El término espacio, también puede referirse a: En astronomía y exploración espacial: Espacio exterior,… … Wikipedia Español
Espacio de configuración — Saltar a navegación, búsqueda En mecánica clásica y mecánica lagrangiana, el espacio de configuración es el espacio de todas las posibles posiciones instantáneas de un sistema mecánico. El espacio de configuración de un sistema mecánico tiene… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Espacio de estados

Espacio de estados

Contenido

Variables de estado