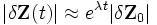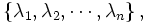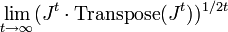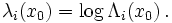Exponente de Lyapunov

Exponente de Lyapunov

Exponente de Lyapunov

El Exponente Lyapunov o Exponente característico Lyapunov de un sistema dinámico es una cantidad que caracteriza el grado de separación de dos trayectorias infinitesimalmente cercanas. Cuantitativamente, dos trayectorias en el espacio-fase con separación inicial 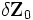\delta \mathbf{Z}_0 diverge

| \delta\mathbf{Z}(t) | \approx e^{\lambda t} | \delta \mathbf{Z}_0 |

El radio de separación puede ser distinto para diferentes orientaciones del vector de separación inicial. Aunque, hay un completo espectro del exponente Lyapunov; el número de ellos es igual al número de dimensiones del espacio-fase. Es común referirse sólo a la más grande, porque determina la predictibilidad de un sistema.

Contenido

Definición

Para un sistema dinámico que evoluciona según la ecuación ft en un espacio de n–dimensiones, el espectro del exponente Lyapunov

\{ \lambda_1, \lambda_2, \cdots , \lambda_n \} \,,

en general depende del punto de inicio x0. El exponente Lyapunov describe el comportamiento de los vectores en el espacio tangente al espacio-fase y son definidos por la matriz Jacobiana:

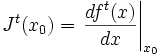J^t(x_0) = \left. \frac{ d f^t(x) }{dx} \right|_{x_0} .

La matriz Jt describe cómo un pequeño cambio en el punto x0 se propaga hasta el punto final ft(x0). El límite

\lim_{t \rightarrow \infty} (J^t \cdot \mathrm{Transpose}(J^t) )^{1/2t}

define a una matriz L(x0) (las condiciones para la existencia del límite son dadas por el teorema de Oseldec. Si Λi(x0) son los valores dados de L(x0), entonces el exponente Lyapunov λi está definido por

\lambda_i(x_0) = \log \Lambda_i(x_0) \,.

Propiedades básicas

  • Si el sistema es conservativo (no existe disipación), la suma de todos los exponentes Lyapunov debe ser cero.
  • Si el sistema es disipativo, la suma será negativa.
  • Si el sistema es un flujo, un exponente será siempre cero.
  • En un sistema dinámico hamiltoniano, la suma sólo puede ser positiva si el sistema es un sistema abierto.
  • El espectro de Lyapunov puede ser usado para estimar el radio de producción de entropía de un sistema dinámico.
  • El inverso del mayor exponente Lyapunov es llamado a veces en literatura momento Lyapunov. Para órbitas caóticas, el momento Lyapunov será finito, aunque para órbitas regulares será infinito.

Cálculo numérico.

Generalmente, el cálculo de los exponentes Lyapunov, como se define arriba, no puede ser llevado a cabo analíticamente, y en la mayoría de los casos uno debe recurrir a técnicas numéricas. Los procedimientos numéricos comúnmente usados estiman la matriz L basándose en un rango finito de aproximaciones de tiempo del límite definiendo L.

Referencias

  • Fernádez Rañada, Antonio (2005). Fondo de Cultura Económica (ed.). Dinámica Clásica, 1ª edición, pp. 545-600. ISBN 84-206-8133-4.

Enlaces externos

Obtenido de "Exponente de Lyapunov"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Exponente Lyapunov — El Exponente Lyapunov o Exponencte característico Lyapunov de un sitema dinámico es una cantidad que caracteriza el radio de separación de dos trayectorias infinitesimalmente cercanas. Cuantitativamente, dos trayectorias en el espacio fase con… …   Enciclopedia Universal

  • Caos determinista — Saltar a navegación, búsqueda El caos y los fractales son parte de un tema mayor, la dinámica, rama de la física que empezó a mediados de 1600 cuando Isaac Newton descubrió las ecuaciones diferenciales, descubrió las leyes de movimiento y la… …   Wikipedia Español

  • Liapunov — o Lyapunov (en ruso Ляпунов) puede hacer referencia a: Prokopi Liapunov (? 1611), estadista ruso. Zajari Liapunov (? después de 1612), estadista ruso, hermano de Prokopi. Mijaíl Liapunov (1820 1868), astrónomo ruso. Aleksandr Liapunov (1857 1918) …   Wikipedia Español

  • Aleksandr Liapunov — Aleksandr Mijáilovich Liapunov (en ruso: Александр Михайлович Ляпунов; 6 de junio (25 de mayo en el calendario juliano) de 1857 – 3 de noviembre de 1918) fue un matemático y físico ruso. Su nombre a menudo se ve transliterado como Lyapunov,… …   Wikipedia Español

  • Billar dinámico — Saltar a navegación, búsqueda El estadio de Bunimovich es un billar dinámico de tipo caótico Un billar dinámico es un sistema dinámico en el cual una partícula alterna entre movimiento rectilíneo y reflexiones especulares en un contorno o… …   Wikipedia Español

  • Caos y fractales — Saltar a navegación, búsqueda La Teoría del Caos surgió cuando Edward Lorenz dio a conocer en 1963 un modelo climático que, por su comportamiento, atrajo la atención de muchos físicos, aunque se basa en trabajos anteriores, como los de Julia,… …   Wikipedia Español

  • Órbita — Para otros usos de este término, véase Órbita (desambiguación). Animación de dos objetos orbitando alrededor de un centro de masas común. En física, una órbita es la trayectoria que describe un objeto alrededor de otro mientras está bajo la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”