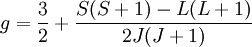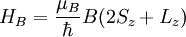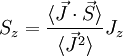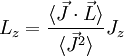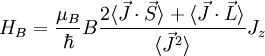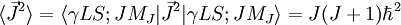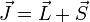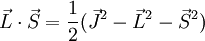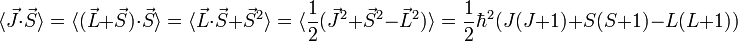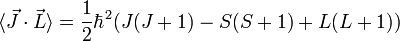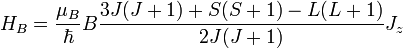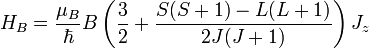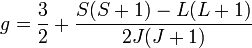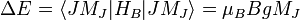Factor de Landé

Factor de Landé

Factor de Landé

En mecánica cuántica existe un efecto llamado Zeeman que consiste en el desdoblamiento de niveles de energía en un átomo cuando se aplica un campo magnético externo. Cuando el campo es lo bastante débil, podemos aplicar teoría de perturbaciones para obtener el valor del desdoblamiento.

El resultado al que se llega es que el aumento (o disminución) en la energía de un nivel concreto depende de los números cuánticos S, L, J y MJ de ese nivel. Si consideramos un campo magnético 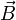\vec{B} paralelo a la dirección espacial Z, obtenemos que la variación de energía correspondiente a un estado propio del hamiltoniano de estructura fina 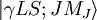| \gamma L S ; J M_J \rangle es

ΔE = μBBgMJ

Donde μB es el magnetón de Bohr y g es el factor de Landé. El factor de Landé viene dado por la expresión

g = \frac{3}{2} + \frac{S (S+1) - L (L+1)}{2J (J+1)}

Obtención del factor de Landé

Vamos a tratar de deducir el valor del factor de Landé a partir del operador hamiltoniano de acoplamiento magnético (perturbación al hamiltoniano de estructura fina). Éste se puede escribir como sigue:

H_B = \frac{\mu_B}{\hbar} B (2S_z + L_z)

Tenemos un problema con la base utilizada. La base de vectores propios del hamiltoniano de estructura fina es la 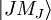| J M_J \rangle. Los operadores Lz y Sz no tienen como base de vectores propios la base 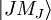| J M_J \rangle. Debemos por tanto expresar estos operadores en función de otros cuya actuación sobre la base 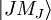| J M_J \rangle sí conozcamos.

Mediante el teorema de proyección, podemos escribir, exclusivamente dentro del subespacio formado por la base \left[ | J M_J \rangle \right] con J fijo, lo siguiente:

S_z = \dfrac{\langle \vec{J} \cdot \vec{S} \rangle}{\langle \vec{J}^2 \rangle} J_z
L_z = \dfrac{\langle \vec{J} \cdot \vec{L} \rangle}{\langle \vec{J}^2 \rangle} J_z

Esto nos permite reescribir HB en la forma

H_B = \frac{\mu_B}{\hbar} B \dfrac{2 \langle \vec{J} \cdot \vec{S} \rangle + \langle \vec{J} \cdot \vec{L} \rangle}{\langle \vec{J}^2 \rangle} J_z

Vayamos por partes. Por un lado, es fácil ver que

\langle \vec{J}^2 \rangle = \langle \gamma L S ; J M_J | \vec{J}^2 | \gamma L S ; J M_J \rangle = J (J + 1) \hbar^2

Por otro, de forma no tan inmediata y a partir de que

\vec{J} = \vec{L} + \vec{S}

y que

\vec{L} \cdot \vec{S} = \frac{1}{2} ( \vec{J}^2 - \vec{L}^2 - \vec{S}^2 )

podemos hacer el siguiente desarrollo:

\langle \vec{J} \cdot \vec{S} \rangle = \langle ( \vec{L} + \vec{S} ) \cdot \vec{S} \rangle = \langle \vec{L} \cdot \vec{S} + \vec{S}^2 \rangle = \langle \frac{1}{2} ( \vec{J}^2 + \vec{S}^2 - \vec{L}^2 ) \rangle = \frac{1}{2} \hbar^2 ( J(J+1) + S(S+1) - L(L+1))

De forma totalmente análoga se llega al resultado

\langle \vec{J} \cdot \vec{L} \rangle = \frac{1}{2} \hbar^2 ( J(J+1) - S(S+1) + L(L+1))

De esta manera, obtenemos la nueva forma de HB:

H_B = \dfrac{\mu_B}{\hbar} B \dfrac{3J(J+1) + S(S+1) - L(L+1)}{2J(J+1)} J_z

Reagrupando, nos queda

H_B = \frac{\mu_B}{\hbar} B \left( \frac{3}{2} + \dfrac{S(S+1) - L(L+1)}{2J(J+1)} \right) J_z

Donde

g = \frac{3}{2} + \dfrac{S(S+1) - L(L+1)}{2J(J+1)}

es el factor de Landé.

La corrección a la energía, por teoría de perturbaciones de primer orden, la obtenemos:

\Delta E = \langle J M_J | H_B | J M_J \rangle = \mu_B B g M_J

que es el resultado al que queríamos llegar.

Referencias

  • Cohen-Tanoudji; Diu; Laloë (1977). Quantum Mechanics, Volume II. Wiley-VCH. ISBN 978-0-471-16435-7.

Enlaces externos

Sitio de donde se ha sacado esta información

Obtenido de "Factor de Land%C3%A9"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Landé-Rotationsfaktor — sukimosi g daugiklis statusas T sritis fizika atitikmenys: angl. rotational g factor vok. Landé Rotationsfaktor, m rus. вращательный множитель Ланде, m pranc. facteur g de rotation, m …   Fizikos terminų žodynas

  • Lande — may refer to:*Lande (surname) *Lande (village), Norway *Château de la Lande, France *Landé g factor …   Wikipedia

  • Landé g-factor — In physics, the Landé g factor is a particular example of a g factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921.In atomic physics, it is a multiplicative term …   Wikipedia

  • Landé’s splitting factor — g daugiklis statusas T sritis fizika atitikmenys: angl. Landé’s splitting factor vok. Aufspaltungsfaktor, m; Landé Faktor, m rus. g фактор, m; множитель Ланде, m; фактор расщепления Ланде, m pranc. facteur de Landé, m; facteur g de Landé, m …   Fizikos terminų žodynas

  • Landé-Faktor — g daugiklis statusas T sritis fizika atitikmenys: angl. Landé’s splitting factor vok. Aufspaltungsfaktor, m; Landé Faktor, m rus. g фактор, m; множитель Ланде, m; фактор расщепления Ланде, m pranc. facteur de Landé, m; facteur g de Landé, m …   Fizikos terminų žodynas

  • Landé-Faktor — atomo g daugiklis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. g factor of atom; g factor of electron vok. Landé Faktor, m; Landéscher g Faktor, m rus. g… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • rotational g-factor — sukimosi g daugiklis statusas T sritis fizika atitikmenys: angl. rotational g factor vok. Landé Rotationsfaktor, m rus. вращательный множитель Ланде, m pranc. facteur g de rotation, m …   Fizikos terminų žodynas

  • g-factor (physics) — For the acceleration related quantity in mechanics, see g force. A g factor (also called g value or dimensionless magnetic moment) is a dimensionless quantity which characterizes the magnetic moment and gyromagnetic ratio of a particle or nucleus …   Wikipedia

  • Alfred Landé — (13 December, 1888 ndash;30 October 1976) was a German American physicist known for his contributions to quantum theory. He is responsible for the Landé g factor and an explanation of the Zeeman Effect.Life and AchievementsAlfred Landé was born… …   Wikipedia

  • G-factor — For the acceleration related quantity in mechanics, see g force. A g factor (also called g value or dimensionless magnetic moment) is a dimensionless quantity which characterizes the magnetic moment and gyromagnetic ratio of a particle or nucleus …   Wikipedia

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”