Forma cuadrática

Forma cuadrática

Forma cuadrática

Una forma cuadrática es una aplicación ω del espacio vectorial E en el cuerpo K, que cumple las siguientes condiciones equivalentes:

a) Existe una forma bilineal simétrica f de 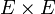E \times E en el cuerpo K tal que ω(x) = f(x,x). A f se le llama forma polar de ω.
b) ω(lx) = l2ω(x), 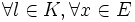\forall l \in K,\forall x \in E. Además f(x,y) = (ω(x + y) − ω(x) − ω(y)) / 2 es una forma bilineal simétrica definida en 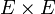E \times E y con valores en K. A ω se la llama forma cuadrática asociada a f.

Una forma cuadrática es por tanto un aplicación 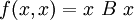f(x,x)=x\ B\ x que es un polinomio de segundo grado con varias variables. Se le puede considerar un caso específico de forma bilineal.

Propiedades y ejemplos

  • Cuando 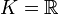K=\mathbb{R} se dice que la forma cuadrática es real.
  • Dos formas cuadráticas pueden ser:
    • Linealmente equivalentes en \mathbb{R} si las signaturas de ambas formas cuadráticas coinciden.
    • Linealmente equivalentes en 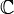\mathbb{C} si los rangos de las matrices de las formas cuadráticas coinciden.
    • Métricamente equivalentes si poseen el mismo polinomio característico.
  • Una forma cuadrática define un espacio vectorial euclídeo si y sólo si es definida positiva, lo cual se puede comprobar utilizando el criterio de Sylvester.

Signatura

La signatura de una forma cuadrática q:V-->R se llama al par (p,m) donde p es el número de elementos positivos que posee la diagonal de la matriz diagonal asociada a q, y m los negativos. Se designa sg (q) y se verifica:

                  p + m = rg (q)
Obtenido de "Forma cuadr%C3%A1tica"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Función cuadrática — En matemáticas, una función cuadrática o función de segundo grado es una función polinómica de grado dos definida como: Gráficas de funciones cuadráticas. en donde a, b y c son números reales (constantes) y a es …   Wikipedia Español

  • Problema de la asignación cuadrática — Saltar a navegación, búsqueda Contenido 1 Origen 2 Definición 3 Modelo Matemático 4 …   Wikipedia Español

  • Ley de reciprocidad cuadrática — En matemática, dentro de la teoría de números la ley de reciprocidad cuadrática designa al teorema áureo que relaciona la solubilidad de dos congruencias de segundo grado relacionadas: donde p y q son números primos impares.[1] …   Wikipedia Español

  • ecuación cuadrática — Ecuación algebraica de particular importancia en la optimización. Un nombre más descriptivo es el de ecuación polinomial (ver polinomio) de segundo grado. Su forma estándar es ax2 + bx + c = 0, y su solución queda determinada por la fórmula… …   Enciclopedia Universal

  • Teorema de equipartición — Figura 1. Movimiento térmico de un péptido tipo hélice α. El movimiento vibratorio es aleatorio y complejo, y la energía de un átomo en particular puede fluctuar ampliamente. Sin embargo, el teorema de equipartición permite que se pueda calcular… …   Wikipedia Español

  • Álgebra de Clifford — Las álgebras de Clifford son álgebras asociativas de importancia en matemáticas, en particular en teoría de la forma cuadrática y del grupo ortogonal y en la física. Se nombran así por William Kingdon Clifford. Definición formal Sea V un espacio… …   Wikipedia Español

  • Equilibrio mecánico — El equilibrio mecánico es un estado estacionario en el que se cumple alguna de estas dos condiciones: Un sistema está en equilibrio mecánico cuando la suma de fuerzas y momentos sobre cada partícula del sistema es cero. Un sistema está en… …   Wikipedia Español

  • Criba de Sundaram — Saltar a navegación, búsqueda La criba de Sundaram es una tabla de los números naturales impares compuestos compuesto por progresiones aritméticas organizadas en las columnas. La criba se basa en el principio de que, al determinar el conjunto de… …   Wikipedia Español

  • Tensor de curvatura — En geometría diferencial, el tensor de curvatura de Riemann , o simplemente tensor de curvatura o tensor de Riemann, supone una generalización del concepto de curvatura de Gauss, definido para superficies, a variedades de dimensiones arbitrarias …   Wikipedia Español

  • Transformada de Legendre — Interpretación geométrica de la Transformada de Legendre. En matemática se dice que dos funciones diferenciables f y g son una transformada de Legendre si cada una de sus primeras derivadas son función inversa de la otra: Se dice entonces de f …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”