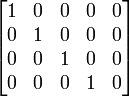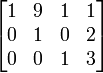En algebra lineal una matriz está en forma REF (forma de filas en escalón) si

• Todas las filas no nulas están por encima de las filas todo ceros, y
• El coeficiente dominante (también llamado pivote) de una fila está siempre a la derecha del coeficiente dominante de la fila superior.

En alguna bibliografía se añade una tercera condición:

• El coeficiente dominante de cada fila no nula es uno.^[1]

Una matriz está en forma RREF (forma de filas en escalón reducida) si satisface las tres condiciones anteriores, y además

• Todo coeficiente dominante es igual a 1 y además es el único elemento no nulo de su columna.

El primer elemento no nulo de cada fila se llama pivote.

Contenido 1 Ejemplos 2 Existencia y unicidad 3 Sistemas de ecuaciones lineales 4 Pseudocódigo 5 Véase también 6 Notas

Ejemplos

Esta matriz está en forma RREF:

La matriz siguiente está en forma REF, pero no en forma RREF:

Sin embargo, esta matriz no está en forma REF, ya que el coeficiente dominante de la fila 3 no está a la derecha del coeficiente dominante de la fila 2.

Existencia y unicidad

Se pueden encontrar infinitas transformaciones REF de una matriz no nula. Sin embargo, todas ellas se corresponden con una única transformación RREF.

Sistemas de ecuaciones lineales

Se dice que un sistema lineal de ecuaciones está en forma escalón si su matriz aumentada está en forma escalón. Análogamente, un sistema lineal de ecuaciones está en forma escalón reducida si su matriz aumentada está en forma escalón reducida.

Pseudocódigo

El siguiente pseudocódigo transforma una matriz a su forma RREF:

function ToReducedRowEchelonForm(Matrix M) is
    lead := 0
    rowCount := the number of rows in M
    columnCount := the number of columns in M
    for 0 ≤ r < rowCount do
        if columnCount ≤ lead then
            stop
        end if
        i = r
        while M[i, lead] = 0 do
            i = i + 1
            if rowCount = i then
                i = r
                lead = lead + 1
                if columnCount = lead then
                    stop
                end if
            end if
        end while
        Swap rows i and r
        Divide row r by M[r, lead]
        for 0 ≤ i < rowCount do
            if i ≠ r do
                Subtract M[i, lead] multiplied by row r from row i
            end if
        end for
        lead = lead + 1
    end for
end function

Véase también

• Eliminación_de_Gauss
• Eliminación_de_Gauss-Jordan

Notas

1. ↑ Larson and Hostetler, Precalculus, 7th edition.