Horizonte de sucesos

Horizonte de sucesos

En relatividad general, el horizonte de sucesos —también llamado horizonte de eventos— se refiere a una hipersuperficie frontera del espacio-tiempo, tal que los eventos a un lado de ella no pueden afectar a un observador situado al otro lado. Obsérvese que esta relación no tiene por qué ser simétrica o biyectiva, es decir, si A y B son las dos regiones del espacio tiempo en que el horizonte de eventos divide el espacio, A puede no ser afectada por los eventos dentro de B, pero los eventos de B generalmente sí son afectados por los eventos en A. Por dar un ejemplo concreto, la luz emitida desde uno de los lados del horizonte de eventos jamás podría alcanzar a un observador situado al otro lado.

Existen diversos tipos de horizontes de eventos, y estos pueden aparecer en diversas circunstancias. Una de ellas particularmente importante sucede en presencia de agujeros negros, aunque este no es el único tipo de horizonte de eventos posibles, existiendo además horizontes de Cauchy, horizontes de Killing, horizontes de partícula u horizontes cosmológicos.

Contenido

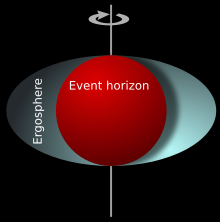
Horizonte de sucesos de un agujero negro rotativo

Esquema del horizonte de sucesos y la ergosfera

El horizonte de sucesos es una superficie imaginaria de forma esférica que rodea a un agujero negro, en la cual la velocidad de escape necesaria para alejarse del mismo coincide con la velocidad de la luz. Por ello, ninguna cosa dentro de él, incluyendo los fotones, puede escapar debido a la atracción de un campo gravitatorio extremadamente intenso.

Las partículas del exterior que caen dentro de esta región nunca vuelven a salir, ya que para hacerlo necesitarían una velocidad de escape superior a la de la luz y, hasta el momento, la teoría indica que nada puede alcanzarla.

Por tanto, no existe modo de observar el interior del horizonte de sucesos, ni de transmitir información hacia el exterior. Esta es la razón por la cual los agujeros negros no tienen características externas visibles de ningún tipo, que permitan determinar su estructura interior o su contenido, siendo imposible establecer en qué estado se encuentra la materia desde que rebasa el horizonte de sucesos hasta que colapsa en el centro del agujero negro.

Si cayéramos en un agujero negro, en el momento de atravesar el horizonte de sucesos no notaríamos ningún cambio, ya que no se trata de una superficie material, sino de una frontera imaginaria, alejada de la zona central donde se concentra la masa. La característica peculiar de esta frontera es que representa el punto de no retorno, a partir del cual no puede existir otro suceso más que caer hacia el interior, dando así origen al nombre de esta superficie.

Al incluir efectos cuánticos en el horizonte de sucesos, se hace posible la emisión de radiación por parte del agujero negro debido a las fluctuaciones del vacío que dan origen a la llamada radiación de Hawking.

Horizonte de un observador acelerado

Otro tipo de horizonte diferente es que es el que ve un observador uniformemente acelerado. Para caracterizar este tipo de horizonte necesitamos introducir las coordenadas de Rindler para el espacio-tiempo de Minkowski. Partiendo de las coordenadas cartesianas la métrica de dicho espacio-tiempo:

ds^2 = -dT^2 + dX^2 + dY^2 + dZ^2, \; \; -\infty < T, X, Y, Z < \infty

Consideremos ahora la región conocida como "cuña de Rindler", dada por el conjunto de puntos que verifican:

\mathcal{R}_{Rind} = \{(T,X,Y,Z)\in\R^4| 0 < X < \infty, \; -X < T < X\}

Y definamos sobre ella un cambio de coordenadas dado por:

t = \operatorname{arctanh}(T/X), \; x= \sqrt{X^2-T^2}, \; y = Y, \; z = Z

Cuya transformación inversa viene dada por:

T = x \, \sinh(t), \; X = x \, \cosh(t), \; Y = y, \; Z = z

Usando estas coordenadas la cuña de Rindler del espacio de Minkowski tiene una métrica expresada en las nuevas coordenadas dada por la expresión:

ds^2 = -x^2 dt^2 + dx^2 + dy^2 + dz^2, \; 0 < x < \infty, -\infty < t, y, z < \infty

Esta métrica tiene una singularidad aparente en x = 0, donde el tensor expresado en las coordenas de Rindler tiene un determinante que se anula. Esto sucede porque en x \rightarrow 0 la aceleración asociada al observador se hace infinita. En estas coordenadas el horizonte de Rindler es precisamente la frontera de la cuña de Rindler. Es interesante que puede demostrarse que este horizonte es análogo en muchos aspectos al horizonte de eventos de un agujero negro.

Horizonte en el universo observable

El límite del universo observable es una hipersuperficie que constituye la barrera de lo que que puede ser observado en cada instante de tiempo, más allá existirían partículas cuya luz todavía no ha tenido tiempo de alcanzarnos, debido a que la edad del universo es finita (ver Big Bang). Todo suceso actual o pasado situado tras el horizonte de eventos, no forma parte del universo observable actual (aunque puede ser visible en el futuro cuando las señales luminosas procedentes de ellos alcancen nuestra posición futura).

La forma en que este horizonte del universo observable cambia según la naturaleza de la expansión del universo. Si la expansión tiene ciertas caracteristicas, que no serán nunca observables, por ejemplo, sin importar cuanto tiempo transcurra (eso pasa en cierto tipo de expansión acelerada, por ejemplo). La frontera pasada de los eventos que nunca podrán ser observados es propiamente un horizonte de sucesos llamado horizonte de sucesos de partícula.

El criterio para determinar si el horizonte de sucesos del universo es diferente del vacío es el siguiente, defínase una distancia comóvil dE mediante la expresión:

d_E=\int_{t_0}^\infty \frac{c}{a(t)}dt\ .

En esta ecuación, a(t) es el factor de escala, c es la velocidad de la luz y t0 es la edad actual del universo. Si d_E \rightarrow \infty, es decir, los puntos arbitrariamente lejanos pueden ser observados, entonces el horizonte de sucesos es vacío. Si d_E \neq \infty entonces existirá un horizonte de sucesos.

Ejemplos de modelos cosmológicos sin horizonte de sucesos son los modelos de universos dominados por materia o por radiación. Un ejemplo de modelo cosmológico con horizonte de sucesos es un universo dominado por la constante cosmológica, como por ejemplo un Universo de De Sitter.

Horizonte de sucesos y topología

El estudio de la causalidad en relatividad general se lleva a cabo siguiendo un enfoque topológico, así un horizonte de eventos futuro o pasado puede caracterizarse como el conjunto de puntos de la clausura topológica del dominio de dependencia de una hipersuperficie lumínica situada en el "infinito" que no pertenecen al pasado o futuro cronológico de dicho dominio. Conviene aclarar que cuando se dice que una hipersuperficie está ubicada en el "infinito" se quiere decir que está situada sobre los puntos del diagrama conforme de Penrose que representa el espacio-tiempo, en signos los horizontes de eventos pasado H^-(\mathcal{S}_L) y futuro H^+(\mathcal{S}_L) de una hipersuperficie lumínica \mathcal{S}_Lvienen dados por:

H^-(\mathcal{S}_L) = \overline{D^-(\mathcal{S}_L)} - I^+(D^-(\mathcal{S}_L)) \qquad H^+(\mathcal{S}_L) = \overline{D^+(\mathcal{S}_L)} - I^-(D^+(\mathcal{S}_L))

Donde la definición de los signos que aparecen es la misma usada en glosario de relatividad.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Horizonte de sucesos — El horizonte de sucesos es la superficie de forma esférica que rodea a un agujero negro. En el horizonte de sucesos la velocidad de escape es igual que la velocidad de la luz. Así, cualquier cosa dentro de él, incluyendo a los fotones, no pueden… …   Enciclopedia Universal

  • Horizonte (desambiguación) — El término horizonte puede hacer referencia a: horizonte terrestre, línea que aparentemente separa el cielo y la tierra. horizonte astronómico, plano que pasa por el observador y es perpendicular a la vertical. horizontes del suelo, serie de… …   Wikipedia Español

  • Problema del horizonte — Saltar a navegación, búsqueda Mapa de la alta isotropías de la radiación de fondo de microondas obtenida por el satélite WMAP, una de las evidencias que conducen al problema del horizonte. El problema del horizonte es una dificultad de los… …   Wikipedia Español

  • Agujero negro — El núcleo de la galaxia elíptica gigante M87, donde hay evidencia de un agujero negro supermasivo. También se observa un potente chorro (jet) de materia eyectada por los poderosos campos magnéticos generados por éste. Imagen tomada por el… …   Wikipedia Español

  • Agujero negro de Kerr-Newman — Un agujero negro de Kerr Newman o agujero negro en rotación con carga eléctrica es aquel que se define por tres parámetros: la masa M, el momento angular J y la carga eléctrica Q. Esta solución fue obtenida en 1960 por los matemáticos Roy Kerr y… …   Wikipedia Español

  • Agujero negro de Reissner-Nordström — Un agujero negro de Reissner Nordstrøm es un agujero negro estático, con simetría esférica y con carga eléctrica, viene definido por dos parámetros: la masa M y la carga eléctrica Q. Su solución fue obtenida en 1918 por el matemático Hans Reißner …   Wikipedia Español

  • Agujero negro de Kerr — Agujero negro de Kerr. Un agujero negro de Kerr o agujero negro en rotación es una región de agujero negro presente en el espacio tiempo de Kerr, cuando el objeto másico tiene un radio inferior a cierta magnitud, por encima de este radio el… …   Wikipedia Español

  • Leonard Susskind — Nombre …   Wikipedia Español

  • Singularidad espaciotemporal — Para otros usos de este término, véase Singularidad. Una singularidad, de modo informal y desde un punto de vista físico, puede definirse como una zona del espacio tiempo donde no se puede definir alguna magnitud física relacionada con los campos …   Wikipedia Español

  • Movimiento rectilíneo uniformemente acelerado — Evolución respecto del tiempo de la posición, de la velocidad y de la aceleración de un cuerpo sometido a un movimiento rectilíneo uniformemente acelerado, según la mecánica clásica. El movimiento rectilíneo uniformemente acelerado (MRUA),… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”