- Isocuanta
-
Mapa de isocuantas, donde se representan tres curvas isocuantas, cada una de la cuales informa de un volumen de producción, Q1, Q2 y Q3, cada uno más elevado que el anterior. X e Y representan dos factores productivos cualesquiera, usualmente capital y trabajo.
En el estudio de la producción, en microeconomía, una isocuanta ( del griego isos=igual y del latín=quanta= cantidades) representa diferentes combinaciones de factores que proporcionan una misma cantidad de producto. Para alcanzar un determinado nivel de producto se puede realizar como resultado de diferentes combinaciones de los factores productivos, dependiendo del método que se utilice.
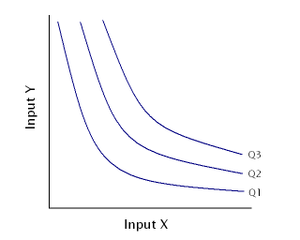
En la representación gráfica habitual, se supone la existencia de dos factores productivos (en el gráfico serían factor X y factor Y) que pueden ser combinados técnicamente de distintas formas, cada punto de la curva representa una combinación distinta de estos factores; y toda la curva, infintas posibilidades de combinar dichos factores. El resultado final siempre es la misma cantidad de producto o producto final terminado.
Una isocuanta de producción es la curva que representa un espacio de insumos (todos variables) que muestran todas las combinaciones posibles de dos o más insumos o factores de producción que son físicamente capaces de generar un mismo nivel o volúmen de producción. Una segunda definición sería: aquélla curva que muestra la combinación, de dos factores productivos, por lo general, Capital (K) y Trabajo (L), que puede producir un determinado nivel o volumen de producción. Se asume que el Trabajo y el Capital son compatibles para producir determinado bien, independientemente de las proporciones en que ambos se utilicen.
Características
- Las isocuantas no se intersecan.
- Son convexas al origen.
- El mapa de isocuantas es denso. Aunque solo trazaremos una o dos isocuantas en el mapa de coordenadas, el espacio constituye un universo de posibles isocuantas.
- Tienen pendiente negativa dentro de las posibilidades eficientes de producción.
- Dan una medida cardinal de producción.
- Las curvas más altas se refieren a niveles más altos de producción, e inversa.
Mapa de Isocuantas
Dos o más curvas isocuantas registradas en un mismo diagrama dan origen a un "mapa de isocuantas". El espacio muestral del mapa permite dibujar infinitas combinaciones de insumos que darían origen a infinitas curvas isocuantas.
Si una empresa desea estudiar distintos niveles de producción, debe entonces trazar un mapa de posibilidades con varias isocuantas. Las isocuantas brindan importante información a la empresa para poder responder a las variaciones de precios en los mercados. Además, en el análisis de toma de decisiones, el conocimiento de dichas curvas pueden ayudar a escoger entre varias alternativas de producción para escoger la combinación que mejor se adecúa en un momento dado para obtener los mejores rendimientos de los distintos factores que afecta dicha curva, para el elevar la eficiencia de la empresa..
Véase también
Wikimedia foundation. 2010.
