Ley de Titius-Bode

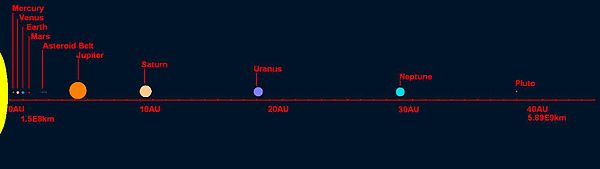
La ley de Titius-Bode, a veces denominada sólo ley de Bode, relaciona la distancia de un planeta al Sol con el número de orden del planeta mediante una regla simple. Matemáticamente, se trata de una sucesión que facilita la distancia de un planeta al Sol.

La ley original era

$a = \frac{n+4}{10}$

donde n = 0, 3, 6, 12, 24, 48..., con cada valor de n dos veces el valor anterior y a representa el semieje mayor de la órbita. Es decir; formemos la sucesión: 0, 3, 6, 12, 24, 48, 96..., Ahora añadamos 4 a la sucesión anterior: 4, 7, 10, 16, 28, 52, 100,... Dividamos por 10 la sucesión anterior: 0,4; 0,7; 1,0; 1,6; 2,8; 5,2; 10,0 ...

En aquella época sólo se conocían los planetas clásicos Mercurio, Venus, Tierra, Marte, Júpiter y Saturno que distan del Sol: 0,38; 0,72; 1; 1,52; 5,2; 9,54 unidades astronómicas

Contenido

1 Descubrimiento e importancia histórica
2 Formulaciones modernas de la ley de Bode
3 Otra forma de expresar la ley de Bode
- 3.1 El problema de Plutón
4 Aplicación a otros sistemas de satélites
5 Referencias
6 Enlaces externos

Descubrimiento e importancia histórica

Johann Daniel Titius.

Johann Elert Bode.

La ley la descubrió en 1766 Johann Daniel Titius y se la atribuyó en 1772 el director del Observatorio de Berlín, Johann Elert Bode; de ahí el nombre. Sin embargo, algunos dicen que el primero en proponerla fue Christian Wolff en 1724.

El descubrimiento de Urano por William Herschel en 1781, que estaba a 19,18 UA, no hizo más que confirmar la ley publicada sólo tres años antes y llevó a que en el quinto lugar a 2,8 UA faltara un planeta. En el congreso astronómico que tuvo lugar en Gotha, Alemania, en 1796, el francés Joseph Lalande recomendó su búsqueda. Entre cinco astrónomos se repartieron el zodiaco en la búsqueda del quinto planeta y finalmente el 1 de enero de 1801, en el Observatorio de Palermo el monje Giuseppe Piazzi, que no pertenecía a la comisión de búsqueda, descubrió Ceres, el primero de los asteroides. El día 3 de enero el cuerpo se había desplazado un tercio de luna hacia el oeste. Hasta el 24 no publicó su descubrimiento, creyendo que era un cometa. Carl Friedrich Gauss, que llegó a ser un gran matemático, inventó ex profeso para Ceres un procedimiento de cálculo de la órbita con tal de aprovechar los pocos datos de la órbita conseguidos por Piazzi. Calculada su órbita, resultó un cuerpo que orbitaba entre Marte y Júpiter; es decir, el cuerpo que faltaba según la ley de Bode.

La ley de Bode, aun pudiendo ser sólo una curiosidad matemática, tuvo una gran importancia en el desarrollo de la Astronomía de finales del siglo XVIII y principios del siglo XIX. Sin embargo, actualmente sólo debe verse como un recurso mnemotécnico y no como un cálculo astronómico exacto.^[1]

Formulaciones modernas de la ley de Bode

La formulación moderna es que la distancia de un planeta al Sol en UAs es:

$a = 0,4 + 0,3\times k$

donde k =0,1,2,4,8,16,32,64,128...=0,2⁰,2¹,2²,2³...

Para los planetas exteriores, el primer término es despreciable, y la interpretación es que cada planeta está aproximadamente dos veces como lejos del sol como el último. Es decir, las distancias de los planetas están prácticamente en progresión geométrica.

Las distancias de los planetas calculados por la ley de Bode comparadas con las reales son:

Planeta	k	Distancia ley T-B	Distancia real
Mercurio	0	0,4	0,39
Venus	1	0,7	0,72
Tierra	2	1,0	1,00
Marte	4	1,6	1,52
Ceres¹	8	2,8	2,77
Júpiter	16	5,2	5,20
Saturno	32	10,0	9,54
Urano	64	19,6	19,2
Neptuno	n/a²		30,06
Plutón	128	38,8	39,44

¹ Ceres es el mayor objeto perteneciente al Cinturón de Asteroides, y tiene que ser considerado un planeta para cubrir el hueco de k=8; por lo tanto, es el número tomado como referencia para la distancia al Sol (2,77 UA). Durante aproximadamente 70 años después de su descubrimiento fue considerado el quinto planeta del sistema solar, pero después del avistamiento de otros objetos de gran tamaño, pasó a ser denominado el asteroide más grande del Cinturón. En el año 2006 se le dio categoría de Planeta enano .

² Neptuno viola la ley, cayendo a medio camino entre el k=64 y k=128.

Otra forma de expresar la ley de Bode

$a = 0,4 + 0,3\times k$

$a = 0,4 + 0,3\times 2^{n-2}$ con n=2,3,4....

Para el caso n=2 a=0,4

Despreciando el 0,4 y colocando unos valores a ajustar:

$a = p\times q^{n-2}$

Tomando logaritmos:

$\log a =\log p + (n-2)\times \log q$

y operando:

$\log a =n\times r+s$

Es decir, tomando logaritmos de las distancias, podemos ajustar por mínimos cuadrados a una recta.

Para los planetas exteriores, si los logaritmos de las distancias siguen una progresión aritmética es porque las distancias siguen una progresión geométrica. Bode pensaba que la razón de la progresión geométrica era 2, pero cuando se hace el ajuste resulta ser solamente 1,71.

El resultado es, considerando a Plutón y tomando como unidad de distancia el km:

$\log a =0,233058\times n +7,5119$ con n=1,2,3,4,5,6,7,8,9,10

y una correlación r=0,9971.

Para expresarlo en logaritmos neperianos hay que multiplicar por 1/M=2,30258 resulta:

$\ln a =0,53663\times n +17,2967$ con n=1,2,3,4,5,6,7,8,9,10

así que las distancias:

$a =e^{0,53663\times n +17,2967}$ con n=1,2,3,4,5,6,7,8,9,10

Si usamos la unidad astronómica

$\log a =0,233058 \times n -0,662989$ con n=1,2,3,4,5,6,7,8,9,10

El cambio, en la unidad no cambia la pendiente ni la correlación, pero la ordenada en el origen queda disminuida en:

$\log U.A. =\log 1,496 \times 10^8= 8,17493$

así 7,5119-8,1749=-0,6630

Así:

$\ln a =0,53663\times n -1,52658$ con n=1,2,3,4,5,6,7,8,9,10

por lo que:

$a =e^{0,53663\times n -1,52658}$ con n=1,2,3,4,5,6,7,8,9,10

así que:

$a =0,21727 \times (1,71023)^n$ con n=1,2,3,4,5,6,7,8,9,10

y comparado ley de Bode clásica:

$a =0,3 \times (2)^{n-2}+0,4$ con n=1,2,3,4,5,6,7,8,9,10

Queda claro que el error de Bode era pensar que cada planeta está al doble de la distancia, cuando en realidad es sólo de 1,71 veces.

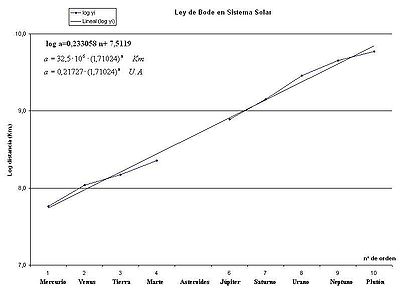Ajuste lineal logarítmico a las distancias de los planetas del Sistema Solar.

Podemos comparar ambas leyes con los valores reales:

Denominación	n	a (U.A.)	a Bode	a (log)
Mercurio	1	0,387	0,4	0,372
Venus	2	0,723	0,7	0,636
Tierra	3	1,000	1	1,087
Marte	4	1,523	1,6	1,859
Ceres¹	5	2,767	2,8	3,179
Júpiter	6	5,203	5,2	5,437
Saturno	7	9,539	10	9,299
Urano	8	19,184	19,6	15,903
Neptuno	9	30,060	n/a²	27,198
Plutón	10	39,759	38,8	46,514

Esta nueva manera de ver las cosas tiene varias ventajas:

El primer término de la sucesión (Mercurio) siempre era especial; ahora es uno más.
El término 0,4 se coloca para ajustar los planetas interiores; aquí es inexistente.
Para Neptuno no se cumplía; ahora sí.

El problema de Plutón

Se puede considerar que Plutón no es un planeta, ya que pertenece al Cinturón de Kuiper. Es un plutino; es decir, pertenece a los asteroides transneptunianos que están en resonancia 3/2 con Neptuno, lo que significa que cada 3 vueltas de Neptuno al Sol el asteroide da 2 vueltas. Ello supone un periodo para el asteroide T=3/2 * 164,7900 años=247,185 años. Por la tercera ley de Kepler a= T^2/3=39,3865 U.A. y una relación de distancias: 39,386/30,06=1,31 por debajo de la media.

Si consideramos que Plutón no es planeta y lo quitamos del ajuste y usamos la unidad astronómica:

$\ln a =0,5497 \times n -1,5723$ con n=1,2,3,4,5,6,7,8,9

así que:

$a =0,2075 \times (1,7327)^n$ con n=1,2,3,4,5,6,7,8,9

Cuando originalmente se publicó, la ley era satisfecha por todos los planetas conocidos -desde Mercurio hasta Saturno- con un hueco entre el cuarto y quinto planeta. Se consideró interesante, pero de ninguna gran importancia hasta el descubrimiento de Urano en 1781, qué encajó pulcramente en la serie. Basado en su nueva credibilidad, Bode inició la búsqueda del quinto planeta. Ceres, el más grande de los asteroides en el Cinturón de Asteroides, se encontró a 2,8 UA, ocupando la quinta posición de esta ley.

Aplicación a otros sistemas de satélites

Hay sólo un limitado número de sistemas en que la ley de Bode puede probarse. Júpiter, Saturno y Urano tienen varias lunas grandes que aparecen haber sido creadas por un proceso similar al que creó los planetas. En la aplicación a los satélites debemos tener presente que deben descartarse todos aquellos que no han sido formados en las proximidades del planeta sino capturados por la gravedad de este. Estos cuerpos se caracterizan por ser pequeños, girar en un plano muy distinto de los satélites grandes o incluso tener un movimiento retrógrado.

Aplicación a los satélites de Júpiter

Los cuatro satélites galileanos de Júpiter más el satélite interno más grande, Amaltea, cumplen perfectamente la ley de Bode:

$\log a =0,2417 \times n +5,0724$ con n=1,2,3,4,5

y una correlación r=0,9925.

Amaltea hay que considerarlo porque a pesar de tener sólo 200 km gira en la órbita de los satélites galileanos.

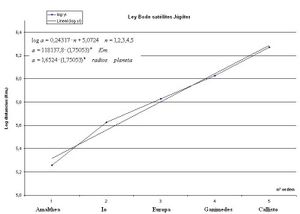Ajuste lineal logarítmico a las distancias de los satélites de Júpiter.

Resulta que

$a =e^{0,55992 \times n +11,6796}$

$a =118137,8 \times (1,75053)^n$

En radios del planeta:

$a =1,6524 \times (1,75053)^n$

Observemos que de un planeta al siguiente en el Sistema Solar o en los Satélites de Júpiter el valor es muy similar.

Para quien tenga dudas, podemos, al igual que Bode, crear una sucesión:

0,3,6,12,24 formada por el 0 y una progresión geométrica con primer término 3 y razón 2.

Ahora añadimos 3 a cada uno de los términos:

3,6,9,15,27

Las distancias de los cinco satélites a Júpiter en radios del planeta son:

2.5, 5.9, 9.4, 15.0, 26.3 el ajuste es perfecto.

Si consideramos sólo los 4 satélites galileanos, el ajuste es todavía más perfecto:

$\log a =0,21423\times n +5,4024$ con n=1,2,3,4

y una correlación r=0,99873.

En radios del planeta:

$a =3,53276 \times (1,63768)^n$

Aplicación a los satélites de Urano

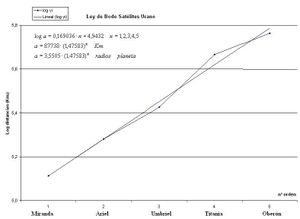Ajuste lineal logarítmico a las distancias de los satélites de Urano.

Las lunas grandes de Urano tienen una adaptación a la ley de Bode magnífica:

$\log a =0,169036\times n +4,9432$ con n=1,2,3,4,5

y una correlación r=0,9943. Es decir:

$a =87738 \times (1,47583)^n$ en km

En radios del planeta:

$a =3,5505524 \times (1,47583)^n$

Mientras que los primeros satélites están a unos 3 radios del planeta, Mercurio está a 83,24 radios solares. No obstante, el crecimiento tiene una tasa bastante similar.

Aplicación a los satélites de Saturno

La aplicación a las lunas de Saturno presenta más problemas. Lo que se ha hecho es ajustar a los satélites grandes más internos (Jano, Mimas, Encelado, Tetis, Dione y Rea) con n=1 hasta 6. Ahora ajustamos los demás hasta que caigan sobre la recta. Hace falta dejar los huecos 7 y 8 hasta llegar a Titán e Hiperión, que serían n=9 y 10 respectivamente. Japeto sería el n=13 y Febe el n=18.

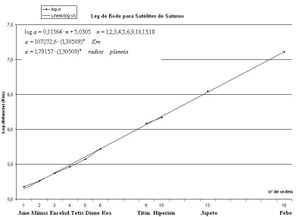Ajuste lineal logarítmico a las distancias de los satélites de Saturno.

Con ello el ajuste sería:

$\log a =0,11564\times n +5,0305$ con n=1,2,3,4,5,6,9,10,13,18

y una correlación de 0,9995.

Es decir:

$a =107272,6 \times (1,30509)^n$ en km

En radios del planeta:

$a =1,79157 \times (1,30509)^n$

Aplicación a planetas extrasolares

Con el avance en las técnicas de descubrimiento de planetas extrasolares ya se han descubierto varios sistemas planetarios sobre los que es posible aplicar la ley. Un reciente estudio de aficionado^[2] trata de aplicar la ley a algunos de estos sistemas, la conclusión es que Kepler 11 y HD 10180 cumplen perfectamente la ley, el estudio consigue aplicarla también a Gliese 876, Gliese 581 y 55Cnc suponiendo la existencia de algunos planetas que no conoceríamos.

Referencias

↑ Gallo, Joaquín; Anfossi, Agustín: Cosmografía, 7ª Edición, Editorial Progreso, México, 1980, página 167.
↑ http://jorgeherber.wordpress.com/2011/05/28/la-ley-de-titius-bode-en-exoplanetas/

Enlaces externos

La ley inexplicable Excelente artículo, fácil de entender, acerca de la Ley de Titius-Bode.
La ley de Titius-Bode Con una posible explicación del fenómeno que hace que en un sistema planetario sólo permanezcan los planetas que cumplen dicha ley.
La ley de Titius-Bode, donde se muestra la La ley de Bode como ajuste lineal del logaritmo de la distancia y su ampliación a los satélites del Sistema Solar.
The Titius-Bode Number Sequence Deciphered Artículo en inglés donde se ofrece una visión de la Ley de Bode exclusivamente del Sistema Solar pero se cambia el punto de vista geocéntrico (Tierra=1) por una unidad que es la distancia Sol-Mercurio=1. Luego se centra en calcular la relación de distancias de un planeta a su anterior llegando a la conclusión de que ésta relación es casi constante y por tanto explicando que las distancias forman una progresión geométrica.

Categorías:

Sistema Solar
Teorías científicas obsoletas
Mecánica celeste

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Bode (desambiguación) — Saltar a navegación, búsqueda El término Bode puede referirse a: Geografía Bode, parroquia del concejo asturiano de Parres en España. Bode (Iowa), localidad del Condado de Humboldt en el Estado de Iowa, Estados Unidos. El Río Bode, que nace en… … Wikipedia Español
Johann Elert Bode — Johann Elert Bode. Johann Elert Bode, (Hamburgo, 19 de enero de 1747 † Berlín, 23 de noviembre de 1826) fue un astrónomo alemán. A pesar de haber sido un gran observador, su carrera se vio inmersa en una interminable serie de polémicas por la… … Wikipedia Español
Johann Daniel Titius — Nacimiento 2 de enero de 1729 Konitz (Chojnice), Royal Prussia … Wikipedia Español
Bode, ley de — Regla que entrega las distancias aproximadas del Sol a los planetas. Enunciada en 1766 por el alemán Johann Daniel Titius (n. 1729–m. 1796), fue popularizada a partir de 1772 por su compatriota Johann Elert Bode (n. 1747–m. 1826). Puede… … Enciclopedia Universal
Cinturón de asteroides — Imagen esquemática del cinturón de asteroides. Se muestra el cinturón principal, entre las órbitas de Marte y Júpiter, y el grupo de los troyanos, en la órbita de Júpiter … Wikipedia Español
Ceres (planeta enano) — Para otros usos de este término, véase Ceres. Ceres Descubrimiento … Wikipedia Español
Sistema Solar — Esquema del Sistema Solar que incluye los planetas y planetas enanos. Los tamaños se encuentran a escala, las distancias entre los planetas y la ubicación no, debido a que una reproducción a escala es imposible por las distancias entre sí … Wikipedia Español
Planeta — Para otros usos de este término, véase Planeta (desambiguación). Planetas del Sistema Solar a escala y ordenados con respecto a su distancia con el Sol. Los planetas son: 1: Mercurio, 2: Venus, 3: Tierra, 4: Marte, 5: Júpiter, 6: Saturno, 7:… … Wikipedia Español
Astronomía — Para otros usos de este término, véase Astronomía (desambiguación). El Hubble: telescopio ubicado fuera de la atmósfera que observa objetos celestes. Sus maravillosas imágenes han asombrado al mundo. Es el icono de la astronomía moderna. La… … Wikipedia Español
Faetón (planeta) — Saltar a navegación, búsqueda Heinrich Wilhelm Matthäus Olbers, quien formuló la hipótesis del planeta Faetón Faetón es el nombre de un planeta hipotético existente entre las órbitas de Marte y Júpiter, cuya destrucción supuestamente llevó a la… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Ley de Titius-Bode

Contenido

Descubrimiento e importancia histórica

Formulaciones modernas de la ley de Bode