En matemática discreta y en particular en la teoría de grafos, un matching o conjunto independiente de aristas (también llamado emparejamiento o apareamiento) en un grafo es un conjunto de aristas independientes, es decir, sin vértices en común.

Definición

Dado un grafo 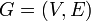un matching M en G es un conjunto de aristas no adyacentes entre sí.

Decimos que un vértice está matched (acoplado, apareado o saturado) si es incidente con una arista en el matching. En otro caso, el vértice está unmatched (libre).

Un matching máximo es un matching que contiene el número máximo posible de aristas. Pueden haber muchos matchings máximos. El número de matching de un grafo es el tamaño del matching máximo.

Un matching maximal es un matching M de un grafo G con la propiedad de que si alguna arista que no pertenece a M es añadido a M, no será ya un matching. Nótese que todos los matching máximos deben ser maximales, pero no todos los matching maximales deben de ser máximos.

Un matching perfecto es un matching que cubre todos los vértices del grafo. Ésto es, cada vértice está saturado bajo el matching. Cada matching perfecto es máximo y maximal.

Dado un matching M

• una trayectoria M-alternante es una trayectoria en la cual sus aristas alternativamente pertenecen y no pertenecen al matching.
• una trayectoria M-aumentante es una trayectoria M-alternante que comienza y termina en un vértice libre (unmatched).

Nótese que un matching es máximo si y sólo si no contiene ninguna trayectoria M-aumentante.

Matchings en grafos bipartitos

Los problemas de matching tienen relación muchas veces con grafos bipartitos. Encontrar un matching máximo bipartito (a menudo llamado cardinalidad máxima de un grafo bipartito) en un grafo bipartito 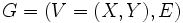es quizás el problema más simple. El algoritmo de los caminos aumentantes lo encuentra por búsqueda de caminos aumentantes por cad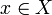a a 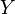y añadiéndolo al matching si existe. Como cada camino puede ser encontrado en tiempo 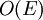, el costo de tiempo es 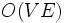. Todas las aristas con flujo de 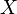a 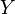constituyen un matching máximo. Una mejora sobre esto es el algoritmo de Hopcroft-Karp, de costo de tiempo .

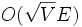En un grafo bipartito ponderado, cada arista tiene asociado un valor. Un matching máximo bipartito ponderado está definido como un matching perfecto donde la suma de los valores de sus arcos en el matching tiene un valor maximal. Si el grafo no es completamente bipartito, los arcos ausentes son introducidos con valor cero. Encontrar tal matching es conocido como problema del asignamiento. Para resolverlo se usa la búsqueda del camino mínimo modificado con el algoritmo del camino aumentante. Si usamos el algoritmo de Bellman-Ford, con costo de tiempo 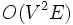. El más especializado es el algoritmo Húngaro que resuelve el problema de asignación con costo de tiempo .

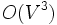Propiedades

• ^[1] Para un grafo G con n vértices con un vértice aislado el número de matching + número de aristas de covering = n
• Un grafo con n vértices y un matching perfecto tiene un número de matching igual a n/2

Véase también

• Conjunto de vertices independientes
• Descomposición de Dulmage-Mendelsohn

Referencias

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 26.3: Maximum bipartite matching, pp.664–669.
• West, Douglas Brent (1999). «3», Introduction to Graph Theory, 2nd edition edición, Prentice Hall. ISBN 0-13-014400-2.