Grafo

Grafo etiquetado con 6 vértices y 7 aristas.

En matemáticas y ciencias de la computación, un grafo (del griego grafos: dibujo, imagen) o gráfica es el principal objeto de estudio de la teoría de grafos.

Informalmente, un grafo es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto.

Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas).

Desde un punto de vista práctico, los grafos permiten estudiar las interrelaciones entre unidades que interactúan unas con otras. Por ejemplo, una red de computadoras puede representarse y estudiarse mediante un grafo, en el cual los vértices representan terminales y las aristas representan conexiones (las cuales, a su vez, pueden ser cables o conexiones inalámbricas).

Prácticamente cualquier problema puede representarse mediante un grafo, y su estudio trasciende a las diversas áreas de las ciencias exactas y las ciencias sociales.

Historia y problema de los puentes de Königsberg

Los siete puentes de Königsberg.

El primer artículo científico relativo a grafos fue escrito por el matemático suizo Leonhard Euler en 1736. Euler se basó en su artículo en el problema de los puentes de Königsberg. La ciudad de Kaliningrado, originalmente Königsberg, es famosa por sus siete puentes que unen ambas márgenes del río Pregel con dos de sus islas. Dos de los puentes unen la isla mayor con la margen oriental y otros dos con la margen occidental. La isla menor está conectada a cada margen por un puente y el séptimo puente une ambas islas. El problema planteaba lo siguiente: ¿es posible, partiendo de un lugar arbitrario, regresar al lugar de partida cruzando cada puente una sola vez?

Abstrayendo este problema y planteándolo con la (entonces aún básica) teoría de grafos, Euler consigue demostrar que el grafo asociado al esquema de puentes de Königsberg no tiene solución, es decir, no es posible regresar al vértice de partida sin pasar por alguna arista dos veces.

De hecho, Euler resuelve el problema más general: ¿qué condiciones debe satisfacer un grafo para garantizar que se puede regresar al vértice de partida sin pasar por la misma arista más de una vez? Si definimos como "grado" al número de líneas que se encuentran en un punto de un grafo, entonces la respuesta al problema es que los puentes de un pueblo se pueden atravesar exactamente una vez si, salvo a lo sumo dos, todos los puntos tienen un grado par.

Definiciones

Un grafo G es un par ordenado G = (V,E), donde:

• V es un conjunto de vértices o nodos, y
• E es un conjunto de aristas o arcos, que relacionan estos nodos.

Normalmente V suele ser finito. Muchos resultados importantes sobre grafos no son aplicables para grafos infinitos.

Se llama orden del grafo G a su número de vértices, | V | .

El grado de un vértice o nodo V es igual al número de arcos E que se encuentran en él.

Un bucle es una arista que relaciona al mismo nodo; es decir, una arista donde el nodo inicial y el nodo final coinciden.

Grafo no dirigido

Grafo no dirigido

Un grafo no dirigido o grafo propiamente dicho es un grafo G = (V,E) donde:

• 
• es un conjunto de pares no ordenados de elementos de .

Un par no ordenado es un conjunto de la forma {a,b}, de manera que {a,b} = {b,a}. Para los grafos, estos conjuntos pertenecen al conjunto potencia de V de cardinalidad 2, el cual se denota por .

Grafo dirigido

Grafo dirigido

Un grafo dirigido o digrafo es un grafo G = (V,E) donde:

• 
• es un conjunto de pares ordenados de elementos de .

Dada una arista (a,b), a es su nodo inicial y b su nodo final.

Por definición, los grafos dirigidos no contienen bucles.

Un grafo mixto es aquel que se define con la capacidad de poder contener aristas dirigidas y no dirigidas. Tanto los grafos dirigidos como los no dirigidos son casos particulares de este.

Pseudografo

Un pseudografo es un grafo G = (V,E) donde:

• 
• es un conjunto de pares no ordenados de elementos de .

Es decir, un pseudografo es un grafo no dirigido que acepta bucles en .

Pseudografo dirigido

Un pseudografo dirigido es un grafo G = (V,E) donde:

• 
• es un conjunto de pares ordenados y etiquetados de elementos de

Es decir, un pseudografo dirigido es un grafo dirigido que acepta bucles en .

Variantes sobre las definiciones principales

Algunas aplicaciones requieren extensiones más generales a las dos propuestas clásicas de grafos. Aunque la definición original los permite, según la aplicación concreta pueden ser válidos o no. A veces V o E pueden ser un multiconjunto, pudiendo haber más de una arista entre cada par de vértices. La palabra grafo (a secas) puede permitir o no múltiples aristas entre cada par de vértices, dependiendo del autor de la referencia consultada. Si se quiere remarcar la inexistencia de múltiples aristas entre cada par de vértices (y en el caso no dirigido, excluir bucles) el grafo puede llamarse simple. Por otra parte, si se quiere asegurar la posibilidad de permitir múltiples aristas, el grafo puede llamarse multigrafo (a veces se utiliza el término pseudografo para indicar que se permiten tanto bucles como múltiples aristas entre cada par de vértices).

Propiedades

• Adyacencia: dos aristas son adyacentes si tienen un vértice en común, y dos vértices son adyacentes si una arista los une.
• Incidencia: una arista es incidente a un vértice si ésta lo une a otro.
• Ponderación: corresponde a una función que a cada arista le asocia un valor (costo, peso, longitud, etc.), para aumentar la expresividad del modelo. Esto se usa mucho para problemas de optimización, como el del vendedor viajero o del camino más corto.
• Etiquetado: distinción que se hace a los vértices y/o aristas mediante una marca que los hace unívocamente distinguibles del resto.

Ejemplos

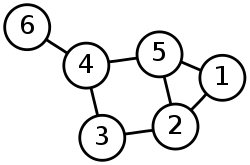
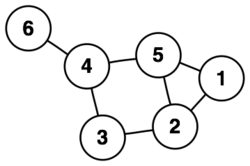
La imagen es una representación del siguiente grafo:

• V:={1,2,3,4,5,6}
• E:={{1,2},{1,5},{2,3},{2,5},{3,4},{4,5},{4,6}}

El hecho que el vértice 1 sea adyacente con el vértice 2 puede ser denotado como 1 ~ 2.

• En la Teoría de las categorías una categoría puede ser considerada como un multigrafo dirigido, con los objetos como vértices y los morfismos como aristas dirigidas.
• En ciencias de la computación los grafos dirigidos son usados para representar máquinas de estado finito y algunas otras estructuras discretas.
• Una relación binaria R en un conjunto X es un grafo dirigido simple. Dos vértices a, b en X están conectados por una arista dirigida ab si aRb.

Grafos particulares

Existen grafos que poseen propiedades destacables. Algunos ejemplos básicos son:

• Grafo nulo: aquel que no tiene vértices ni aristas. Nótese que algunas personas exigen que el conjunto de vértices no sea vacío en la definición de grafo.
• Grafo vacío: aquel que no tiene aristas.
• Grafo trivial: aquel que tiene un vértice y ninguna arista.
• Grafo simple: aquel que no posee bucles o lazos.
• Grafo completo: grafo simple en el que cada par de vértices están unidos por una arista, es decir, contiene todas las posibles aristas.
• Grafo bipartito completo: sea (W,X) una partición del conjunto de vértices V, es aquel donde cada vértice en W es adyacente sólo a cada vértice en X, y viceversa.
• Grafo bipartito: sea (W,X) una partición del conjunto de vértices V, es aquel donde cada arista tiene un vértice en W y otro en X.
• Grafo plano: aquel que puede ser dibujado en el plano cartesiano sin cruce de aristas.
• Árbol: grafo conexo sin ciclos.

Una generalización de los grafos son los llamados hipergrafos.

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Grafo. Commons