- NURBS
-
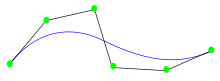
Las superficies tridimensionales NURBS pueden tener formas orgánicas complejas. Los puntos de control influyen en la dirección que tome la superficie. El cuadrado mas exterior delinea los grados en X/Y de la superficie. Modelado y renderizado en Cobalt.
Una curva NURBS.
Versión animadaNURBS (acrónimo inglés de la expresión Non Uniform Rational B-splines) es un modelo matemático muy utilizado en la computación gráfica para generar y representar curvas y superficies.
Historia
El desarrollo de NURBS empezó en 1950 por ingenieros que necesitaban la representación matemática precisa de superficies de forma libre como las usadas en carrocerías de automóviles, superfices de exteriores aeroespaciales y cascos de barcos, que pudieran ser reproducidos exacta y técnicamente en cualquier momento. Las anteriores representaciones de este tipo de diseños sólo podían hacerse con modelos físicos o maquetas realizadas por el diseñador o ingeniero.
Los pioneros en esta investigación fueron Pierre Bézier quien trabajaba como ingeniero en Renault, y Paul de Casteljau quien trabajaba en Citroën, ambos en Francia. Bézier y Casteljau trabajaron casi en paralelo, aunque ninguno de los dos conoció el trabajo que el otro desarrollaba. Bezier publicó primero sus trabajos y por esta razón tradicionalmente se le ha asociado a las Bézier-Splines (splines de Bézier, que son representadas con puntos de control describiendo a la curva misma), mientras que el nombre de Casteljau sólo es conocido por los algoritmos que desarrolló para la evaluación de superficies paramétricas. En la década de 1960 se desarrollaron las NURBS (B-splines Racionales No Uniformes), y se convirtieron en la generalización de las Bézier splines.
Las primeras NURBS fueron usadas en paquetes propietarios de CAD de las compañías automotrices. Posteriormente formaron parte del estándar en paquetes de gráficos por computadora. En 1985, el primer modelador interactivo de NURBS para PC, llamado Macsurf (posteriormente Maxsurf), fue desarrollado por Formation Design Systems, una pequeña compañía en Australia. Maxsurf es un sistema de diseño para cascos, que pretendía la creación de barcos, botes y yates, para los diseñadores quienes tenían la necesidad de alta precisión en el esculpido de superficies. Actualmente las aplicaciones más profesionales de gráficos por computadora para equipos de escritorio ofrecen la tecnología.
Referencias
- Les Piegl & Wayne Tiller: The NURBS Book, Springer-Verlag 1995–1997 (2nd ed.). The main reference for Bézier, B-Spline and NURBS; chapters on mathematical representation and construction of curves and surfaces, interpolation, shape modification, programming concepts.
- Dr. Thomas Sederberg, BYU NURBS, http://cagd.cs.byu.edu/~557/text/ch5.pdf
- Dr. Lyle Ramshaw. Blossoming: A connect-the-dots approach to splines, Research Report 19, Compaq Systems Research Center, Palo Alto, CA, June 1987
- David F. Roger: An Introduction to NURBS with Historical Perspective, Morgan Kaufmann Publishers 2001. Good elementary book for NURBS and related issues.
- Foley, van Dam, Feiner & Hughes: Computer Graphics - Principles and Practice, Addison Wesley 1996 (2nd ed.).
Enlaces externos
- Acerca de los Nonuniform Rational B-Splines - NURBS, En inglés.
- Una introducción interactiva a los NURBS, En inglés.
- NURBS with 3ds max tutorials (en)
- http://www.cs.bris.ac.uk/Teaching/Resources/COMS30115/all_9.pdf
- http://devworld.apple.com/dev/techsupport/develop/issue25/schneider.html
- http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/AV0405/DONAVANIK/bezier.html
- http://mathcs.holycross.edu/~croyden/csci343/notes/Lecture33_CurvesIII.ppt
- http://www.opennurbs.com/
- http://www.rhino3d.com/nurbs.htm/
- http://www.npowersoftware.com/
Categorías:- Software de gráficos
- Splines
- Acrónimos
Wikimedia foundation. 2010.
