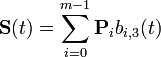- B-spline
-
B-spline
En el subcampo matemático de análisis numérico, una B-spline es una función spline que tiene el mínimo apoyo con respecto a un determinado grado, suavidad, y partición del dominio. Un teorema fundamental establece que cada función spline de un determinado grado, suavidad, y partición del dominio, se puede representar como una combinación lineal de B-splines del mismo grado y suavidad, y sobre la misma partición.[1] El término B-spline fue acuñado por Isaac Jacob Schoenberg y es la abreviatura de spline básica.[2] Las B-splines pueden ser evaluadas de una manera estable numéricamente por el algoritmo de Boor.
En el subcampo de informática de diseño asistido por computadora y de gráficos por computadora, el término B-spline se refiere con frecuencia a una curva spline parametrica por funciones spline que se expresan como combinaciones lineales de B-splines (en el sentido matemático anterior). Una B-spline es simplemente una generalización de una curva de Bézier, que puede evitar el fenómeno Runge sin necesidad de aumentar el grado de la B-spline.
Contenido
Definición
Dado m valores reales ti, llamados nudos, con
una B-spline de grado n es una curva paramétrica
compuesta por una combinación lineal de B-splines básicas bi,n de grado n
![\mathbf{S}(t)= \sum_{i=0}^{m-n-2} \mathbf{P}_{i} b_{i,n}(t) \mbox{ , } t \in [t_{n-1},t_{m-n}]](/pictures/eswiki/101/e3d23bd072ccf53f73eb15b1e08a24f6.png) .
.
Los Pi se llaman puntos de control o puntos de Boor. Hay m-(n+1) puntos de control que forman un casco convexo.
Las m-n+1 B-splines básicas de grado n se pueden definir mediante la fórmula de recursión Cox-de Boor
Cuando los nudos son equidistantes, la B-spline se dice que es uniforme, de otro modo seria no uniforme. Si dos nudos tj son idénticos, cualquiera de las posibles formas indeterminadas 0/0 se consideran 0.
Nótese que j+n+1 no puede exceder de m-1, lo que limita tanto a j como a n.
B-spline uniforme
Cuando la B-spline es uniforme, las B-splines básica para un determinado grado n son sólo copias cambiadas de una a otra. Una alternativa no recursiva de la definición de la B-splines m-n+1 básica es
con
y
dónde
es la función de potencia truncada.
B-spline cardinal
Si se define B0 como la función característica de
![[-\tfrac{1}{2}, \tfrac{1}{2}]](/pictures/eswiki/49/19a2ea4a10660560d6779686604a0c8d.png) , y Bk recursivamente como el producto convolución
, y Bk recursivamente como el producto convoluciónentonces Bk se llaman B-splines cardinal (centrada). Esta definición se remonta a Schoenberg.
Bk tiene soporte compacto
![[-\tfrac{k+1}{2}, \tfrac{k+1}{2}]](/pictures/eswiki/52/49f088871626685ab979ba1845c5a7ee.png) y es una función impar. Como
y es una función impar. Como  las B-splines cardinales normalizadas tienden a la función de Gauss [4].
las B-splines cardinales normalizadas tienden a la función de Gauss [4].Notas
Cuando el número de puntos de control de Boor es el mismo que el grado, la B-Spline degenera en una curva de Bézier. La forma de las funciones base es determinada por la posición de los nudos. Escalar o trasladar el vector de nudo no altera las funciones de base.
El spline esta contenido en el casco convexo de sus puntos de control.
Una B-spline básica de grado n
es distinta de cero sólo en el intervalo [ti, ti+n+1] esto es
En otras palabras si manipulamos un punto de control cambiamos sólo el comportamiento local de la curva y no el comportamiento global como con las curvas de Bézier.
La función base se pueda obtener del polinomio Bernstein.
Ejemplos
B-spline constante
La B-spline constante es la spline más simple. Se define en un solo tramo de nudo y ni siquiera es continua en los nudos. Es sólo la función indicador de los diferentes tramos de nudo.
B-spline lineal
La B-spline lineal se define en dos tramos de nudo consecutivos y es continua sobre los nudos, pero no diferenciable.
B-spline cuadrática Uniforme
B-splines cuadráticas con nudo-vector uniforme es una forma común de B-spline. La función de mezclado puede ser calculada fácilmente , y es igual para cada segmento, en este caso.
Puesto en forma de matriz, esto es: http://graphics.idav.ucdavis.edu/education/CAGDNotes/Quadratic-Uniform-B-Spline-Curve-Splitting/Quadratic-Uniform-B-Spline-Curve-Splitting.html
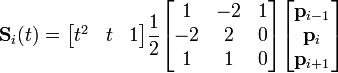 para
para ![t \in [0,1], i = 1,2 \ldots m-1](/pictures/eswiki/99/c525eb4e77ed286a7e4145114dc40cc2.png)
B-spline cúbica
Una formulación B-spline para un solo segmento puede ser escrita como:
donde Si es el imo segmento B-spline y P es el conjunto de puntos de control, el segmento i y k es el índice del punto de control local. Un conjunto de puntos de control sería P
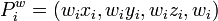 donde el wi es el peso, tirando de la curva hacia el punto de control Pi mientras que aumenta o se desplazan fuera de la curva, mientras que disminuye.
donde el wi es el peso, tirando de la curva hacia el punto de control Pi mientras que aumenta o se desplazan fuera de la curva, mientras que disminuye.Toda una serie de segmentos, las curvas m-2 (S3,S4,...,Sm) definidas por m+1 puntos de control (
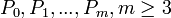 ) como un B-spline en t se definiría como:
) como un B-spline en t se definiría como:donde i es el número de puntos de control y t es un parámetro global dado los valores de los nudos. Esta formulación expresa una curva B-spline como una combinación lineal de funciones B-spline básicas, de ahí el nombre.
Hay dos tipos de B-spline - uniforme y no uniforme. Una B-spline no uniforme es una curva donde los intervalos entre los puntos sucesivos de control no es, o no necesariamente es, iguald (el vector de nudos de espacios de nudo interiores no son iguales). Una forma común es donde los intervalos se reducen sucesivamente a cero, interpolando los puntos de control.
B-splines cúbica uniforme
La B-splines cúbica con vector-nudo uniforme es la forma más usual de B-spline. La función de mezcla puede ser fácilmente calculada, y es igual para cada segmento, en este caso. Puesto en forma de matriz, esto es:
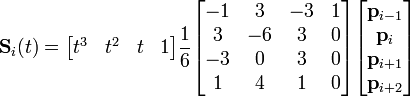 para
para ![t \in [0,1].](/pictures/eswiki/100/de4ef1e33d30a0fa6fc661f8fed20bde.png)
Véase también
References
- ↑ Carl de Boor (1978). A Practical Guide to Splines. Springer-Verlag, pp. 113–114.
- ↑ Carl de Boor (1978). A Practical Guide to Splines. Springer-Verlag, pp. 114–115.
Categoría: Splines
Wikimedia foundation. 2010.

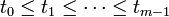
![\mathbf{S}:[t_0, t_{m-1}] \to \mathbb{R}^2](/pictures/eswiki/99/c84ac26cd8497363a5d1b554318cf4f6.png)
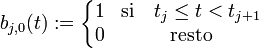
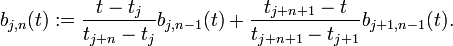

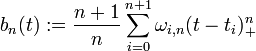
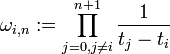
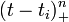
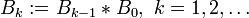
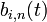
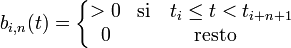
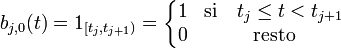
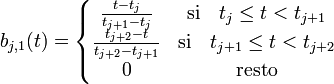
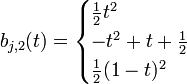
![\mathbf{S}_{i} (t) = \sum_{k=0}^3 \mathbf{P}_{i-3+k} b_{i-3+k,3} (t) \mbox{ ; }\ t \in [0,1]](/pictures/eswiki/101/ed125f5c5449a17aaa556fb6554dca6e.png)