Ordenación topológica

Una ordenación topológica de un grafo acíclico G dirigido es una ordenación lineal de todos los nodos de G que conserva la unión entre vértices del grafo G original. La condición que el grafo no contenga ciclos es importante, ya que no se puede obtener ordenación topológica de grafos que contengan ciclos.

Usualmente, para clarificar el concepto se suelen identificar los nodos con tareas a realizar en la que hay una precedencia a la hora de ejecutar dichas tareas. La ordenación topológica por tanto es una lista en orden lineal en que deben realizarse las tareas.

Para poder encontrar la ordenación topológica del grafo G deberemos aplicar una modificación del algoritmo de búsqueda en profundidad (DFS).

Algoritmos

Los algoritmos usuales para el ordenamiento topológico tienen un tiempo de ejecución de la cantidad de nodos más la cantidad de aristas (O(|V|+|E|)).

Uno de los algoritmos, primero descrito por Kahn (1962), trabaja eligiendo los vértices del mismo orden como un eventual orden topológico. Primero, busca la lista de los "nodos iniciales" que no tienen arcos entrantes y los inserta en un conjunto S; donde al menos uno de esos nodos existe si el grafo es acíclico. Entonces:

L ← Lista vacía que contendrá luego los elementos ordenados.
S ← Conjunto de todos los nodos sin aristas entrantes.

MIENTRAS [S no es vacío]:
        n ← nodo extraído de S
        insertar n en L

        PARA CADA [nodo m con arista e de n a m]:
                e ← arista extraída del grafo

                SI [m no tiene más aristas entrantes]:
                        insertar m en S

SI [el grafo tiene más aristas]:
        error: el grafo tiene al menos un ciclo
SINO:
        RETORNAR L

Si respeta la definición de GAD, ésta es una solución posible, listada en L (no es la única solución). De lo contrario el grafo contiene al menos un ciclo y por lo tanto un ordenamiento topológico es imposible.

Ha de tenerse en cuenta que, debido a la falta de unicidad del orden resultante, la estructura S puede ser simplemente un conjunto, una cola o una pila.

Dependiendo del orden que los nodos "n" son extraídos del conjunto S, hay una diferente posible solución.

Una alternativa al algoritmo visto para ordenamiento topológico está basado en DFS (del inglés búsqueda en profundidad). Para este algoritmo, las aristas están en dirección contraria al algoritmo anterior (y en dirección contraria a lo que muestra el diagrama del ejemplo). Hay un arco desde x a y si la tarea x depende de la tarea y (en otras palabras, si la tarea y debe completarse antes que la tarea x empiece). El algoritmo se repite a través de cada nodo del grafo, en un orden arbitrario, iniciando una búsqueda en profundidad que termina cuando llega a un nodo que ya ha sido visitado desde el comienzo del orden topológico.

La ordenación topológica no es única. Depende en qué orden recorras los nodos del grafo en el bucle for de la función ORDENACIÓN_TOPOLÓGICA. La nomenclatura adicional utilizada es: lista = Estructura de datos lista enlazada

  ORDENACIÓN_TOPOLÓGICA(grafo G)
  for each vertice u ∈ V[G]do
          estado[u] = NO_VISITADO
          padre[u] = NULL
  tiempo =0
  for each vertice u ∈ V[G]do
          if estado[u] = NO_VISITADO then
                  TOPOLÓGICO-Visitar(u)

  TOPOLÓGICO-Visitar(nodo u)
  estado[u]=VISITADO
  tiempo = tiempo+1
  distancia[u] = tiempo
  for each v ∈ Adyacencia[u] do
          if estado[v]=NO_VISITADO then
                  padre[v]=u
                  TOPOLÓGICO-Visitar(v)
  estado[u] = TERMINADO
  tiempo = tiempo+1
  finalización[u] = tiempo
  insertar (lista, u)

Al final de la ejecución del algoritmo se devuelve la lista enlazada de nodos, que corresponde con la ordenación topológica del grafo .

Ejemplos

• En rojo se muestran los siguientes tiempos: distancia[u] / finalización[u]

1. Ejecutamos el algoritmo ORDENACIÓN_TOPOLÓGICA (grafo G) sobre el siguiente grafo.

2. El algoritmo nos devuelve una lista enlazada con los nodos del grafo en orden decreciente en tiempo de finalización.

Grafo ordenado topológicamente. En él se pueden ver claramente las precedencias de las tareas:

• Ponerse la camisa antes que el cinturón y el jersey
• Ponerse el pantalón antes que los zapatos y el cinturón
• Ponerse los calcetines antes que los zapatos

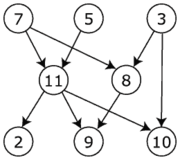
La aplicación canónica del orden topológico es en programación, una secuencia de tareas; los algoritmos de ordenamiento topológico fueron estudiados por primera vez a los comienzos de los años 60 en el contexto de la técnica "PERT" (Técnica de Revisión y Evaluación de Programas del inglés) de programación en gestión de proyectos ((Jarnagin, ,1960)). Las tareas están representados por vértices, y hay un arco (o arista) desde x a y si la tarea x debe completarse antes que la tarea y comience (por ejemplo, cuando se lava la ropa, la lavadora debe terminar antes de ponerla a secar). Entonces, un orden topológico brinda un orden para ejecutar las tareas.

El gráfico muestra que hay muchos tipos de ordenamiento posibles: 7, 5, 3, 11, 8, 2, 9, 10 (visto de izquierda a derecha, de arriba a abajo) 3, 5, 7, 8, 11, 2, 9, 10 (por números menores primero) 3, 7, 8, 5, 11, 10, 2, 9 5, 7, 3, 8, 11, 10, 9, 2 (por menor cantidad de aristas primero) 7, 5, 11, 3, 10, 8, 9, 2 (por números mayores primero) 7, 5, 11, 2, 3, 8, 9, 10

Referencias

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 22.3: Depth-first search, pp.540–549.