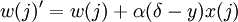El Perceptrón es un tipo de red neuronal artificial desarrollado por Frank Rosenblatt, véase Perceptrón multicapa, también puede entenderse como perceptrón la neurona artificial y unidad básica de inferencia en forma de discriminador lineal, que constituye este modelo de red neuronal artificial, esto debido a que el perceptrón puede usarse como neurona dentro de un perceptrón más grande u otro tipo de red neuronal artificial.

Contenido 1 Definición 2 Aprendizaje 3 Ejemplo 4 Véase también

Definición

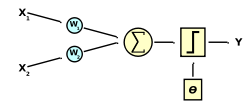
El perceptrón usa una matriz para representar las redes neuronales y es un discriminador terciario que traza su entrada x (un vector binario) a un único valor de salida f(x) (un solo valor binario) a través de dicha matriz.

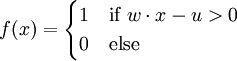
Donde w es un vector de pesos reales y 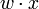es el producto punto (que computa una suma ponderada). u es el 'umbral', el cual representa el grado de inhibición de la neurona, es un término constante que no depende del valor que tome la entrada.

El valor de f(x) (0 o 1) se usa para clasificar x como un positivo o un caso negativo, en el caso de un problema de la clasificación binario. El umbral puede pensarse de como compensar la función de activación, o dando un nivel bajo de actividad a la neurona del rendimiento. La suma ponderada de las entradas debe producir un valor mayor que u para cambiar la neurona de estado 0 a 1.

Aprendizaje

El algoritmo de aprendizaje es el mismo para todas las neuronas, todo lo que sigue se aplica a una sola neurona en el aislamiento. Nosotros definimos algunas variables primero:

• el x(j) denota el elemento en la posición j en el vector de la entrada
• el w(j) el elemento en la posición j en el vector de peso
• el y denota la salida de la neurona
• el δ denota la salida esperada
• el α es una constante tal que 0 < α < 1

Los pesos son actualizados después de cada entrada según la regla de actualización siguiente:

Por lo cual, el aprendizaje es modelado como la actualización del vector de peso después de cada iteración, lo cual sólo tendrá lugar si la salida y difiere de la salida deseada δ. Para considerar una neurona al interactuar en múltiples iteraciones debemos definir algunas variables más:

• x_i denota el vector de entrada para la iteración i
• w_i denota el vector de peso para la iteración i
• y_i denota la salida para la iteración i
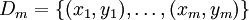• denota un periodo de aprendizaje de m iteraciones

En cada iteración el vector de peso es actualizado como sigue:

• Para cada pareja ordenada (x,y) en
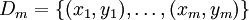
• Pasar (x_i,y_i,w_i) a la regla de actualización w(j)' = w(j) + α(δ − y)x(j)

El periodo de aprendizaje D_m se dice que es separable linealmente si existe un valor positivo γ y un vector de peso w tal que: 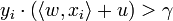para todos los i.

Novikoff (1962) probo que el algoritmo de aprendizaje converge después de un número finito de iteraciones si los datos son separables linealmente y el número de errores esta limitado a: .

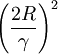Sin embargo si los datos no son separables linealmente, la línea de algoritmo anterior no se garantiza que converja.

Ejemplo

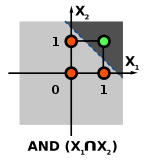
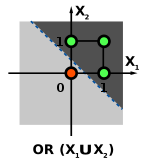
Considere las funciones AND y OR, estas funciones son linealmente separables y por lo tanto pueden ser aprendidas por un perceptrón.

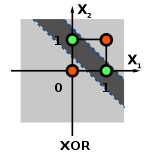
La función XOR no puede ser aprendida por un único perceptrón puesto que requiere al menos de dos líneas para separar las clases (0 y 1). Debe utilizarse al menos una capa adicional de perceptrones para permitir su aprendizaje.

Véase también

• Perceptrón multicapa