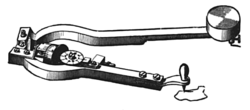
- Planímetro
-
Planímetro
Un planímetro (1908) midiendo el área indicada por trazado de su perímetro.
El planímetro es un instrumento de medición utilizado para el cálculo de áreas irregulares. Este modelo se obtiene en base la teoría de integrales de línea o de recorrido.
Contenido
Contexto
Para los casos en los que se necesita calcular superficies irregulares o en perspectiva, como mapas o manchas la geometría clásica o incluso la geometría analítica no son suficientes y no prestan mayor utilidad. Por ello es necesario recurrir a una herramienta de medición especifica para tal fin, el planímetro es una buena y fácil alternativa.
Modelo y esquema de utilización
Se tiene un origen O, dos longitudes constantes conocidas R y L, y los ángulos variables y respectivamente, que se forman con la horizontal, tal como se muestran en la figura 1.
Figura 1: Esquema de aplicación del planímertro.
Para poder calcular el área A de la sección irregular, según la teoría del cálculo, se emplea una integral de línea en sentido contrario a las manecillas del reloj (para resultado positivo).
Pero el vector r, no es fácilmente implementable en la vida real, ya que se tiene un largo y un ángulo variables. Para simplificar la implementación del vector r, se recurre a la suma de dos vectores cuyo módulo es constante, pero se tendrían dos ángulos variables, los cuales son sencillos de medir.
Obtención del modelo matemático
Para calcular el área de una sección encerrada por una curva c, descrita por la ecuación vectorial r(t) se utiliza: A= (1)
Donde (t)=(x(t),y(t))
Ahora según la figura 1:
x(t) = Rcos() + Lcos() (2) y(t) = Rsen() + Lsen() (3)
Al aplicar (2) y (3) en la ecuación (1), se obtiene:
A= (4)
Conclusiones
La ecuación (4) es fácilmente programable en muchos lenguajes de programación de alto nivel (PASCAL, C, FORTRAN, etc), debido a que sólo se necesita de un muestreo de los ángulos y .
Incluso los ángulos se podrían medir manualmente e ingresar los datos registrados al programa del planímetro.
Véase también
Categorías: Instrumentos de medición | Herramientas matemáticas
Wikimedia foundation. 2010.
