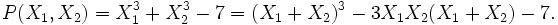Polinomios simétricos

Polinomios simétricos

Polinomios simétricos

En matemáticas, un polinomio simétrico es un anillo de polinomios en n variables P(X1,X2,...,Xn), tal que si intercambiamos alguna de las variables el polinomio sigue siendo el mismo.

Ejemplos

Estos polinomios:

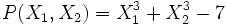
  • P(X_1, X_2) = X_1^3+ X_2^3-7
  • P(X1,X2) = 4X1X2
  • P(X1,X2,X3) = X1X2X3 − 2X1X2 − 2X1X3 − 2X2X3

son todos simétricos. El polinomio P(X1,X2) = X1 − X2 no es simétrico, ya que si intercambiamos X1 y X2 obtenemos el polinomio X2 − X1, que no es el mismo.

Los ladrillos constituyentes de los polinomios simétricos

Para cada n, existen n polinomios simétricos elementales en las variables X1,X2,...,Xn. Son los ladrillos constiyutentes para todos los polinomios simétricos en dichas variables, lo que quiere decir que todo polinomio simétrico en n variables puede obtenerse a partir de estos polinomios elementales mediante multiplicaciones y sumas. Más concretamente: cualquier polinomio simétrico en n variables es un polinomio de los n polinomios elementales simétricos en dichas variables. Por ejemplo, para n=2, sólo hay dos polinomios simétricos elementales, X1 + X2 y X1X2. El primer polinomio de la lista de arriba puede entonces escribirse como sigue:

P(X_1, X_2) = X_1^3+ X_2^3-7=(X_1+X_2)^3-3X_1X_2(X_1+X_2)-7.

Véase también

  • función simétrica - este término es empleado a veces para referirse a los polinomios simétricos.
Obtenido de "Polinomios sim%C3%A9tricos"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Polinomios simétricos — En matemáticas, un polinomio simétrico es un polinomio en n variables , tal que si intercambiamos alguna de las variables el polinomio sigue siendo el mismo …   Enciclopedia Universal

  • Polinomios de Legendre — Saltar a navegación, búsqueda En matemáticas al resolver la formula de Rodrigues, las Funciones de Legendre son las soluciones a las Ecuaciones Diferenciales de Legendre: llamadas así por el matemático francés Adrien Marie Legendre. Estas… …   Wikipedia Español

  • Identidades de Newton — En Matemática, las identidades de Newton, también conocidas como las fórmulas Newton Girard, son dos maneras diferentes de describir la raíz de un polinomio. Concretamente, relacionan las sumas de potencias con los polinomios simétricos… …   Wikipedia Español

  • Teoría de Galois — Évariste Galois (1811–1832) En matemáticas, la teoría de Galois es una colección de resultados que conectan la teoría de cuerpos con la teoría de grupos. La teoría de Galois tiene aplicación a diversos problemas de la teoría de cuerpos, que… …   Wikipedia Español

  • Polinomio homogéneo — En Matemáticas, un polinomio homógeneo es un polinomio cuyo términos son monomios que tienen el mismo total de grados; o sus elementos son de la misma dimensión. Por ejemplo, x5 + 2x3y2 + 9x1y4 es un polinomio homogéneo de grado 5, en dos… …   Wikipedia Español

  • Problema de Galois inverso — Problemas no resueltos de la matemática: Todo polinomio con coeficientes racionales lleva asociado un grupo de Galois, pero ¿es cierto que todo grupo finito es grupo de Galois de algún polinomio? En teoría de Galois, el problema de Galois inverso …   Wikipedia Español

  • Método del gradiente biconjugado estabilizado — En álgebra lineal numérica, el método del gradiente biconjugado estabilizado, generalmente abreviado como BiCGSTAB (del inglés «biconjugate gradient stabilized method»), es un método iterativo propuesto por H. A. van der Vorst para la resolución… …   Wikipedia Español

  • Configuración electrónica — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Número primo — Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores distintos: él mismo y el 1. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de sí mismos y del 1. El número …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”