- Polinomios de Legendre
-
Polinomios de Legendre
En matemáticas al resolver la formula de Rodrigues, las Funciones de Legendre son las soluciones a las Ecuaciones Diferenciales de Legendre:
llamadas así por el matemático francés Adrien-Marie Legendre. Estas ecuaciones se encuentran frecuentemente en Física y en otros campos técnicos. En particular, aparecen cuando se resuelve la ecuación de Laplace (un tipo de ecuación en derivadas parciales) en coordenadas esféricas.
La ecuación diferencial de Legendre puede resolverse usando el método de serie de potencias. En general la serie de potencias obtenida converge cuando |x| < 1 y en el caso particular de que n sea un entero no negativo (0, 1, 2,...) las soluciones forman una familia de polinomios ortogonales llamados Polinomios de Legendre.
Cada polinomio de Legendre Pn(x) es un polinomio de grado n. Éste puede ser expresado usando la Fórmula de Rodrigues:
Una Expresión explícita
Desarrollando la fórmula de Rodrigues se obtiene la siguiente expresión para los Polinomios de Legendre
esta expresión es útil en caso de por ejemplo de querer elaborar un programa que grafique los polinomios de Legendre, de ésta expresión es relativamente fácil obtener una para los Polinomios Asociados de Legendre, que aperecen en la práctica en la resolución de problemas como el átomo de hidrógeno por ejemplo.
La propiedad de ortogonalidad
Una importante propiedad de los polinomios de Legendre es que éstos son ortogonales con respecto al producto escalar definido en L2 en el intervalo −1 ≤ x ≤ 1:
(donde δmn denota la delta de Kronecker, igual a 1 si m = n y 0 para otros casos). De hecho, una derivación alternativa de los polinomios de Legendre es llevando a cabo procesos de Gram-Schmidt en los polinomiales {1, x, x2,...} con respecto a un producto interno. La razón de esta propiedad de ortogonalidad es que la ecuación diferencial de Legendre puede ser vista como un problema de Sturm-Lioville
donde los valores propios λ corresponden a n(n+1).
Ejemplos de polinomios de Legendre
Unos pocos primeros polinomios de Legendre:
n 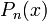
0 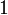
1 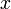
2 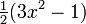
3 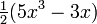
4 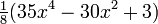
5 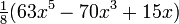
6 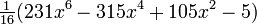
7 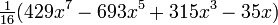
8 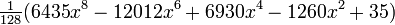
9 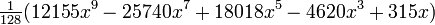
10 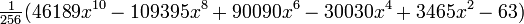
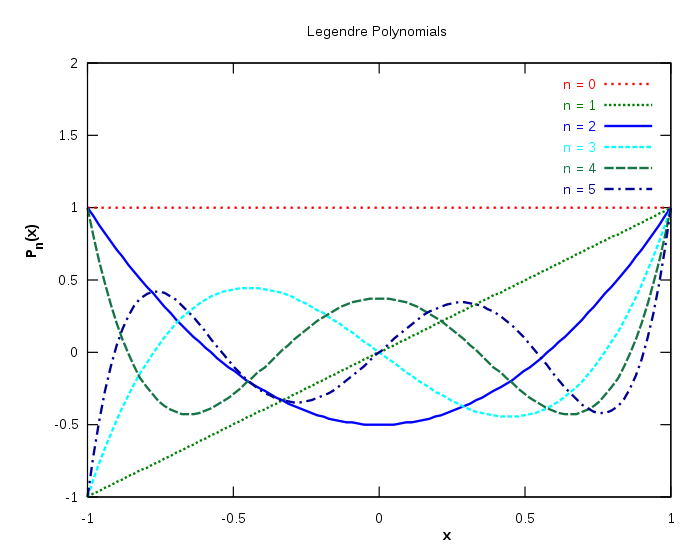
Los gráficos de estos polinomios (menores a n=5) se grafican abajo:
Aplicaciones de los Polinomios de Legendre en Física
Los polinomios de Legendre, igual que los de Hermite y Laguerre, son útiles en ramas de la Física como el Cálculo Numérico ya que permiten el cálculo de integrales definidas sin necesidad de resolver el integrando, tan sólo haciendo que los intervalos de integración vayan desde -1 a +1 (con el correspondiente cambio de variable). Ésto es especialmente interesante en programas de cómputo que tratan de resolver una integral definida.
Los polinomios de Legendre son útiles en la expansión de funciones como
donde r y r' son las longitudes de los vectores
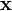 y
y 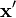 respectivamente y γ es el ángulo entre los dos vectores. La expansión mantiene r > r'. Esta expresión esta usada, por ejemplo, para obtener el potencial de una carga puntual, que se siente en un punto
respectivamente y γ es el ángulo entre los dos vectores. La expansión mantiene r > r'. Esta expresión esta usada, por ejemplo, para obtener el potencial de una carga puntual, que se siente en un punto 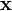 mientras la carga esta localizada en el punto
mientras la carga esta localizada en el punto 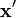 . La expansión usando polinomios de Legendre puede ser útil para integrar esta expresión sobre una carga continua distribuida.
. La expansión usando polinomios de Legendre puede ser útil para integrar esta expresión sobre una carga continua distribuida.Los polinomios de Legendre aparecen en la solución de una Ecuación de Laplace de un potencial,
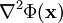 , en una región del espacio de carga libre, usando el método de separación de variables, donde las condiciones limite tienen simetría axial (no depende del ángulo azimuthal). Donde
, en una región del espacio de carga libre, usando el método de separación de variables, donde las condiciones limite tienen simetría axial (no depende del ángulo azimuthal). Donde 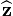 es el eje de simetría y θ es el ángulo entre la posición del observador y el eje
es el eje de simetría y θ es el ángulo entre la posición del observador y el eje 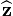 , la solución del potencial podría ser
, la solución del potencial podría ser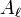 y
y 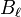 están determinados de acuerdo con las condiciones limite de cada problema.[1]
están determinados de acuerdo con las condiciones limite de cada problema.[1]Polinomios de Legendre en expansión multipolo
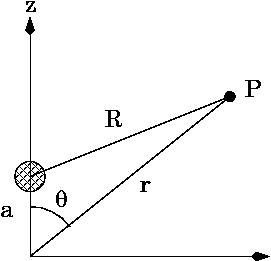 Figure 2
Figure 2Los polinomios de Legendre son también útiles en la expansión de funciones de la forma (esto es similar al caso anterior, escrito un poco diferente):
que aparece naturalmente en expansión multipolo. La parte izquierda de la ecuación es la función generadora de los polinomios de Legendre.
Como en el ejemplo, del potencial eléctrico Φ(r,θ) (en coordenadas esféricas) debido a una carga puntual localizada en el eje z en z = a (Fig. 2) varia como
Si el radio r del punto de observación P es más grande que a, el potencial puede expanderse en polinomios de Legendre
donde se define η = a / r < 1 y x = cosθ. Esta expansión es usada para mejorar la expansión multipolo normal.
Por el contrario, si el radio r del punto de observación P es más pequeño que a, el potencial puede aun ser expandido en los polinomios de Legendre como por encima, pero con a y r cambiados.
Propiedades adicionales de los polinomios de Legendre
Los polinomios de Legendre son simétricos o antisimetricos, tal que
Desde que la ecuación diferencial y la propiedad ortogonal son escalarmente independientes, los polinomios de Legendre definidos son estandarizados (a veces llamados normalizados, pero notese que la real norma no es la unidad) por ser escalar tal que
La derivada en un punto final esta dado por
Los polinomios de Legendre pueden construirse usando las tres relaciones de recurrencia
y
Útil para la integración de polinomios de Legendre es
Traslación de los polinomios de Legendre
La traslación de los polinomios de Legendre
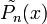 están definidos como un intervalo unitario ortogonal [0,1]
están definidos como un intervalo unitario ortogonal [0,1]Una expresión explicita para estos polinomios viene dado por
La analogía a la Fórmula de Rodríguez para la traslación de los polinomios es:
La primera traslación de los polinomios de Legendre es:
n 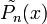
0 1 1 2x − 1 2 6x2 − 6x + 1 3 20x3 − 30x2 + 12x − 1 Polinomios de Legendre de orden fraccional
Los polinomios de Legendre de orden fraccional existen y siguen a la inserción de la derivada fraccional como definición al Cálculo Fraccional y a los factoriales no enteros (definidos por una función gamma) en una Fórmula de Rodrígues. Los exponentes, seguramente, tienen de exponentes fraccionarios que representan raíces.
Véase también
- Cuadratura Gaussiana
- Polinomios asociados de Legendre
- Funciones racionales de Legendre
Enlaces externos
- A quick informal derivation of the Legendre polynomial in the context of the quantum mechanics of hydrogen
- Wolfram MathWorld entry on Legendre polynomials
- Dr James B. Calvert's article on Legendre polynomials from his personal collection of mathematics
Referencias
- ↑ Jackson, J.D. Classical Electrodynamics, 3rd edition, Wiley & Sons, 1999. page 103
Categorías: Ecuaciones diferenciales ordinarias | Polinomios | Funciones especiales
Wikimedia foundation. 2010.

![{d \over dx} \left[ (1-x^2) {d \over dx} P(x) \right] + n(n+1)P(x) = 0.](/pictures/eswiki/57/97426c1b358960a3da8430c9d4b3e931.png)
![P_n(x) = {1 \over 2^n n!} {d^n \over dx^n } \left[ (x^2 -1)^n \right].](/pictures/eswiki/55/70a1790c4fb6b05d9ccea331b0dabe51.png)
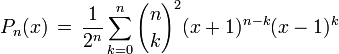
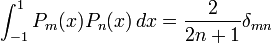
![{d \over dx} \left[ (1-x^2) {d \over dx} P(x) \right] = -\lambda P(x),](/pictures/eswiki/98/b93b0519eba36d1149a5ad46e123f14d.png)
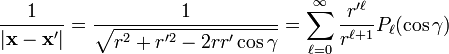
![\Phi(r,\theta)=\sum_{\ell=0}^{\infty} \left[ A_\ell r^\ell + B_\ell r^{-(\ell+1)} \right] P_\ell(\cos\theta).](/pictures/eswiki/100/d3a683c19b5e5e533d574488ec388893.png)
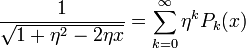
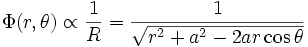
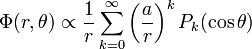
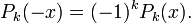
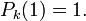
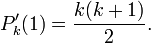
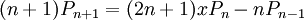
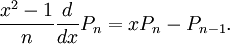
![(2n+1) P_n = {d \over dx} \left[ P_{n+1} - P_{n-1} \right].](/pictures/eswiki/102/f952fd5ea27624b5b8f54f68d7caca68.png)
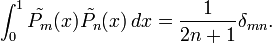
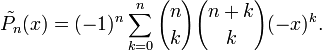
![\tilde{P_n}(x) = ( n!)^{-1} {d^n \over dx^n } \left[ (x^2 -x)^n \right].\,](/pictures/eswiki/98/b74d56e4dd062b9b3fb0267aa33f4aa4.png)