El problema de la parada o problema de la detención para Máquinas de Turing consiste en lo siguiente: dada una Máquina de Turing M y una palabra w, determinar si M se detendrá cuando es ejecutada usando w como dato de entrada. Alan Turing, en su famoso artículo "On Computable Numbers, with an Application to the Entscheidungsproblem" (1936), demostró que el problema de la parada de la Máquina de Turing es indecidible.

Relevancia en la práctica

Al ejecutar un programa, este puede terminar después de un número finito de pasos o puede nunca terminar. En la práctica, este último caso se manifiesta como programas que se quedan "trabados" o que entran a un bucle infinito. Por esta razón sería de gran utilidad resolver la siguiente pregunta en la práctica:

Esta pregunta es, en términos modernos, el problema de la parada. Una forma muy natural de intentar resolver el problema es hacer funcionar el programa p con los datos de entrada x y esperar para ver si termina; sin embargo habría que determinar cuánto tiempo hay que esperar para estar completamente seguros de que p en verdad nunca termina. De hecho, esto es imposible: está demostrado que este problema no se puede solucionar algoritmicamente –es decir, que es irresoluble.

Irresolubilidad del problema

La irresolubilidad del problema se puede mostrar de varias formas, pero en esencia todas equivalen a un argumento diagonal de Cantor. A continuación se muestra el argumento en términos modernos de programación:

Supongamos que este problema sí se puede resolver algoritmicamente; entonces hay un programa, que llamaremos Termina, que cada vez que se le suministra el código de un programa p y sus datos de entrada x, hace un número finito de operaciones y responde "True" cuando el programa termina o "False" cuando el programa nunca termina. En lenguaje Python:

def Termina(p, x):
    #Supongamos que aquí se encuentra un código maravilloso que soluciona el problema de la parada
    #Esta función regresa True si p(x) termina o False en otro caso

Bajo la suposición de que existe este programa, se puede usar como subrutina de otro programa más grande, al que llamaremos "Diagonal" (en referencia a la diagonal de Cantor). Este programa recibirá como dato de entrada el código de un programa cualquiera w, y usará el programa anterior para decidir si el programa w termina cuando se le suministra ella misma como entrada (no hay nada de raro en esto, pues en la práctica hay programas como los compiladores se pueden suministrarse a sí mismos como dato de entrada). A continuación, Diagonal hace lo opuesto: Si w termina entonces Diagonal entra en un ciclo infinito y si w entra en un ciclo infinito entonces Diagonal termina. En lenguaje Python:

def Diagonal(w):
    if Termina(w, w):
        while True: #Estas instrucciones forman un bucle infinito
            pass

Resumiendo, el programa Diagonal está diseñado para tener la siguiente propiedad:

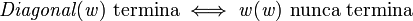
Como w puede ser el código de cualquier programa, particularmente puede ser el del mismo Diagonal:

Diagonal("def Diagonal(w):\n    if Termina(w, w):\n        while True:\n            pass")

En este caso se tiene w = Diagonal, y por lo tanto

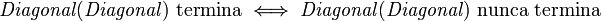
Es decir que bajo la suposición de que existe el algoritmo Termina se llega a la absurda conclusión de que hay una instrucción que termina siempre y cuando no termine. Como esta conclusión es absurda, entonces no puede existir el algoritmo Termina; es decir que es imposible resolver el problema de la parada algoritmicamente.

Referencias

• [Michael] (2005). Introduction to the Theory of Computation, 2 edición, Course Technology. ISBN 978-0534950972.
• [Dean] (1995). Teoría de Autómatas y Lenguajes Formales. Prentice Hall. ISBN 0-13-497777-7.

• George S. Boolos, John P. Burgess & Richard C. Jeffrey (2007). Computability and Logic. Cambridge University Press. ISBN 978-0521701464.