Prueba χ²

Prueba χ²

Prueba χ²

En estadística y estadística aplicada se denomina prueba χ² (pronunciado como "ji-cuadrado" y a veces incorrectamente como "chi-cuadrado") a cualquier prueba en la que el estadístico utilizado sigue una distribución χ² si la hipótesis nula es cierta. Algunos ejemplos de pruebas χ² son:

  • La prueba χ² de Pearson, la cual tiene numerosas aplicaciones:
  • La prueba χ² de frecuencias
  • La prueba χ² de independencia
  • La prueba χ² de bondad de ajuste
  • La prueba χ² de Pearson con corrección por continuidad o corrección de Yates
  • La prueba de Bartlett de homogeneidad de varianzas

Prueba χ² de Pearson

La prueba χ² de Pearson es considerada como una prueba no paramétrica que mide la discrepancia entre una distribución observada y otra teórica (bondad de ajuste), indicando en qué medida las diferencias existentes entre ambas, de haberlas, se deben al azar en el contraste de hipótesis. También se utiliza para probar la independencia de dos variables entre sí, mediante la presentación de los datos en tablas de contingencia.

La fórmula que da el estadístico es la siguiente:

\chi^2=\sum_{i}\frac{(\mathrm{observada}_{i}-\mathrm{teorica}_{i})^2}{\mathrm{teorica}_{i}}

Cuanto mayor sea el valor de χ2, menos verosímil es que la hipótesis sea correcta. De la misma forma, cuanto más se aproxima a cero el valor de chi-cuadrado, más ajustadas están ambas distribuciones.

Los grados de libertad gl vienen dados por :

gl= (r-1)(k-1). Donde r es el número de filas y k el de columnas.

  • Criterio de decisión:

Se acepta H0 cuando 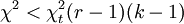\chi^2 < \chi^2_t(r-1)(k-1). En caso contrario se rechaza.

Donde t representa el valor proporcionado por las tablas, según el nivel de significación estadística elegido.

Véase también

Obtenido de "Prueba %CF%87%C2%B2"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • prueba — sustantivo femenino 1. Acción y efecto de probar: Sus superiores pusieron a prueba sus conocimientos y destreza. Irene ha encargado un vestido y va hoy a la primera prueba. 2. Forma de demostrar la verdad o falsedad de algo: No hay luz en la casa …   Diccionario Salamanca de la Lengua Española

  • prueba — 1. f. Acción y efecto de probar. 2. Razón, argumento, instrumento u otro medio con que se pretende mostrar y hacer patente la verdad o falsedad de algo. 3. Indicio, señal o muestra que se da de algo. 4. Ensayo o experimento que se hace de algo,… …   Diccionario de la lengua española

  • Prueba — Saltar a navegación, búsqueda Prueba puede referirse a: Prueba, un hecho utilizado para demostrar una acción, tesis o teoría en ciencias. Prueba en matemáticas. Véase Demostración matemática. Prueba en Lógica. Véase: Cálculo lógico; Deducción;… …   Wikipedia Español

  • prueba AF — Prueba en la que se utiliza una tinción fluorescente para teñir un anticuerpo con el objetivo de identificar muestras clínicas. Los tintes fluorescentes hacen que los organismos teñidos sean visibles cuando se examinan con un microscopio de… …   Diccionario médico

  • prueba — f. med. Experiencia que tiene por objetivo investigar la presencia de una lesión, sustancia o anomalía. ⊆ psicol. Conjunto de procedimientos más o menos estandarizados que permiten determinar las características psíquicas de un sujeto. También se …   Diccionario médico

  • prueba FA — Véase prueba de anticuerpos fluorescentes. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 …   Diccionario médico

  • prueba de AZ — Véase prueba de Ascheim Zondek. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 …   Diccionario médico

  • prueba de FC — Abreviatura de prueba de fijación del complemento. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 …   Diccionario médico

  • prueba de FL — Véase prueba de fijación del látex. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 …   Diccionario médico

  • prueba de PK — Abreviatura de prueba de Prausnitz Küstner. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 …   Diccionario médico

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”