Distribución χ²

Distribución χ² (ji-cuadrado)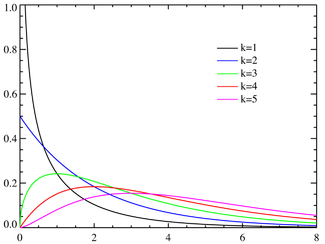
Función de densidad de probabilidad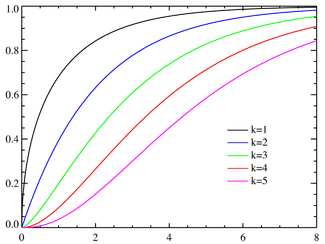
Función de distribución de probabilidad
Parámetros	$k > 0\,$ grados de libertad
Dominio	$x \in [0; +\infty)\,$
Función de densidad (pdf)	$\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}\,$
Función de distribución (cdf)	$\frac{\Gamma(k/2,x/2)}{\Gamma(k/2)}\,$
Media	$k\,$
Mediana	aproximadamente $k-2/3\,$
Moda	$k-2\,$ if $k\geq 2\,$
Varianza	$2\,k\,$
Coeficiente de simetría	$\sqrt{8/k}\,$
Curtosis	$12/k\,$
Entropía	$\frac{k}{2}\!+\!\ln(2\Gamma(k/2))\!+\!(1\!-\!k/2)\psi(k/2)$
Función generadora de momentos (mgf)	$(1-2\,t)^{-k/2}$ for $2\,t<1\,$
Función característica	$(1-2\,i\,t)^{-k/2}\,$

En estadística, la distribución χ² (de Pearson), llamada Chi cuadrado o Ji cuadrado, es una distribución de probabilidad continua con un parámetro $k$ que representa los grados de libertad de la variable aleatoria

$X = Z_1^2 + \cdots + Z_k^2$

donde $Z i$ son variables aleatorias normales independientes de media cero y varianza uno. El que la variable aleatoria $X$ tenga esta distribución se representa habitualmente así: $X\sim\chi^2_k$ .

Es conveniente tener en cuenta que la letra griega χ se transcribe al latín como chi^[1] y se pronuncia en castellano como ji.^[2] ^[3]

Contenido

1 Propiedades
- 1.1 Función de densidad
- 1.2 Función de distribución acumulada
2 Relación con otras distribuciones
3 Aplicaciones
4 Referencias
5 Véase también
6 Enlaces externos

Propiedades

Función de densidad

Su función de densidad es:

$f(x;k)= \begin{cases}\displaystyle \frac{1}{2^{k/2}\Gamma(k/2)}\,x^{(k/2) - 1} e^{-x/2}&\text{para }x\ge0,\\ 0&\text{para }x<0 \end{cases}$

donde $Γ$ es la función gamma.

Demostración

La función densidad de

X 1 = Z 2

si Z es tipo N(0,1) viene dada por

$P(x,x+dx)=f(x_1)dx_1=\frac{1}{\sqrt{2\pi}}e^{-z^2/2}dz$

Despejando y teniendo en cuenta contribuciones positivas y negativas de z:

$f(x_1)=\frac{1}{\sqrt{2\pi}}e^{-x_1/2}x_1^{-\frac{1}{2}}$

La función distribución de $X = X 1 + X 2 + ... + X n$ viene dada por su convolución

$f (x; k) = f (x 1) * f (x 2) * ... * f (x k)$

Aplicando transformada de Laplace

$\mathcal{L}\left \{ f(x;k) \right \} =(\mathcal{L}\left \{ f(x_1) \right \} )^k=\frac{1}{(2(s+\frac{1}{2}))^{\frac{k}{2}}}$

Aplicando antitransformada se obtiene f(x;k)

$f(x;k)=\mathcal{L}^{-1}\left \{ \frac{1}{(2(s+\frac{1}{2}))^{\frac{k}{2}}} \right \}=\frac{1}{2^{k/2}\Gamma(k/2)}\,x^{(k/2) - 1} e^{-x/2}$

Función de distribución acumulada

Su función de distribución es

$F_k(x) = \frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

donde $\ \gamma(k,z)$ es la función gamma incompleta.

El valor esperado y la varianza de una variable aleatoria X con distribución χ² son, respectivamente, k y 2k.

Relación con otras distribuciones

La distribución χ² es un caso especial de la distribución gamma. De hecho, $X \sim \Gamma(\frac{k}{2}, \theta=2).$ Como consecuencia, cuando $k = 2$ , la distribución χ² es una distribución exponencial de media $k = 2$ .

Cuando k es suficientemente grande, como consecuencia del teorema central del límite, puede aproximarse por una distribución normal:

$\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{(1,\sqrt{2/k})} (x)$

Aplicaciones

La distribución χ² tiene muchas aplicaciones en inferencia estadística. La más conocida es la de la denominada prueba χ² utilizada como prueba de independencia y como prueba de bondad de ajuste y en la estimación de varianzas. Pero también está involucrada en el problema de estimar la media de una población normalmente distribuida y en el problema de estimar la pendiente de una recta de regresión lineal, a través de su papel en la distribución t de Student.

Aparece también en todos los problemas de análisis de varianza por su relación con la distribución F de Snedecor, que es la distribución del cociente de dos variables aleatorias independientes con distribución χ².

Referencias

Véase también

Enlaces externos

[1]Calcular la probabilidad de una distribución de Pearson con R (lenguaje de programación)

Categoría:

Distribuciones continuas

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Distribución — Saltar a navegación, búsqueda Distribución es la acción y efecto de distribuir. Aplicado a diferentes campos puede referirse a: Contenido 1 Economía 2 Informática 3 Matemática … Wikipedia Español
Distribución F — Saltar a navegación, búsqueda Fisher Snedecor Función de densidad de probabilidad Función de distribución de probabilidad Parámetros … Wikipedia Español
distribución — sustantivo femenino 1. Acción y resultado de distribuir: distribución de víveres, distribución de medicamentos, distribución del trabajo. La distribución de mercancías empieza a las ocho de la mañana. La distribución del cine hispano debe… … Diccionario Salamanca de la Lengua Española
distribución — (Del lat. distributĭo, ōnis). 1. f. Acción y efecto de distribuir. 2. Com. Reparto de un producto a los locales en que debe comercializarse. 3. Econ. Asignación del valor del producto entre los distintos factores de la producción. 4. Mat. Función … Diccionario de la lengua española
distribución — Localización de las medicaciones en varios órganos y tejidos después de la administración. La concentración de los fármacos altamente hidrosolubles puede ser mayor en personas ancianas, deshidratadas o febriles porque tienen menos agua corporal… … Diccionario médico
Distribución — (Del lat. distributio, onis.) ► sustantivo femenino 1 Acción y resultado de distribuir o distribuirse. 2 Disposición de las diferentes partes y habitaciones de un edificio: ■ esta casa tiene una buena distribución. SINÓNIMO disposición ordenación … Enciclopedia Universal
Distribución F — Usada en teoría de probabilidad y estadística, la distribución F es una distribución de probabilidad contínua. También se la conoce como distribución F de Snedecor o como distribución F de Fisher Snedecor . Una variable aleatoria de distribución… … Enciclopedia Universal
distribución — {{＃}}{{LM D13765}}{{〓}} {{SynD14090}} {{［}}distribución{{］}} ‹dis·tri·bu·ción› {{《}}▍ s.f.{{》}} {{＜}}1{{＞}} Reparto entre varios, designando lo que corresponde a cada uno de acuerdo con cierta regla o derecho, o según dicte la voluntad o la… … Diccionario de uso del español actual con sinónimos y antónimos
distribución — (f) (Básico) todas las actividades que hacen llegar el producto al consumidor Ejemplos: Su empresa se especializa en la distribución de vino español en el mercado polaco. El coste de distribución suele suponer eso de un 30% del precio final.… … Español Extremo Basic and Intermediate
distribución — s f 1 Acto de distribuir o repartir algo: una mala distribución de la riqueza 2 Reparto o entrega: distribución de la leche, distribución del correo 3 Arreglo o disposición que tiene o que s da a algo; forma en que algo se reparte o se extiende… … Español en México

Los diccionarios y las enciclopedias sobre el Académico

Distribución χ²

Contenido