Prueba de Kruskal-Wallis

Prueba de Kruskal-Wallis

Prueba de Kruskal-Wallis

En estadística, la prueba de Kruskal-Wallis (de William Kruskal y W. Allen Wallis) es un método no paramétrico para probar si un grupo de datos proviene de la misma población. Intuitivamente, es idéntico al ANOVA con los datos reemplazados por categorías. Es una extensión de la prueba de la U de Mann-Whitney para 3 o más grupos.

Ya que es una prueba no paramétrica, la prueba de Kruskal-Wallis no asume normalidad en los datos, en oposición al tradicional ANOVA. Si asume bajo la hipótesis nula que los datos vienen de la misma distribución. Una forma común en que se viola este supuesto es con datos heterocedásticos.

Método

  1. Ordenar todos los datos de la muestra de menor a mayor, y asignar al menor un rango de 1, al segundo un 2, y así hasta el n-ésimo. Si existen datos que se repiten, se asigna el rango promedio a cada uno de ellos (si existen cuatro datos idénticos que ocupan los rangos 11, 12, 13 y 14, se les asigna un rango de 12,5 a los cuatro).
  2. El estadístico está dado por: 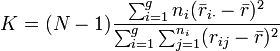K = (N-1)\frac{\sum_{i=1}^g n_i(\bar{r}_{i\cdot} - \bar{r})^2}{\sum_{i=1}^g\sum_{j=1}^{n_i}(r_{ij} - \bar{r})^2}, donde:
    • ng es el número de observaciones en el grupo g
    • rij es el rango (entre todas las observaciones) de la observación j en el grupo i
    • N es el número total de observaciones entre todos los grupos
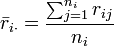    • \bar{r}_{i\cdot} = \frac{\sum_{j=1}^{n_i}{r_{ij}}}{n_i},
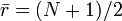    • \bar{r} =(N+1)/2 es el promedio de rij.
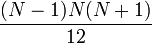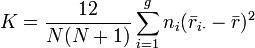      Note que el denominador de la expresión para K es exactamente \frac{(N-1)N(N+1)}{12}. Luego K = \frac{12}{N(N+1)}\sum_{i=1}^g n_i(\bar{r}_{i\cdot} - \bar{r})^2.
  3. Se puede realizar una corrección para los valores repetidos dividiendo K por 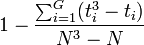1 - \frac{\sum_{i=1}^G (t_{i}^3 - t_{i})}{N^3-N}, donde G es el número de grupos de diferentes rangos repetidos, y ti es el número de observaciones repetidas dentro del grupo i que tiene observaciones repetidas para un determinado valor. Esta corrección hace cambiar a K muy poco al menos que existan un gran número de observaciones repetidas.
  4. Finalmente, el p-value es aproximado por 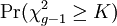\Pr(\chi^2_{g-1} \ge K). Si algún ni es pequeño ( < 5) la distribución de K puede ser distinta de la chi-cuadrado.

Véase también

  • Prueba de Mann-Whitney

Referencias

Artículo adaptado de la Wikipedia en inglés.

  • William H. Kruskal and W. Allen Wallis. Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association 47 (260): 583–621, December 1952.
  • Sidney Siegel and N. John Castellan, Jr. (1988). Nonparametric Statistics for the Behavioral Sciences (second edition). New York: McGraw-Hill.
Obtenido de "Prueba de Kruskal-Wallis"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Kruskal — puede hacer referencia a: Joseph Kruskal, matemático estadounidense. Martin Kruskal, matemático estadounidense hermano del anterior. William Kruskal, matemático y estadístico estadounidense, hermano de los anteriores. Algoritmo de Kruskal,… …   Wikipedia Español

  • Prueba U de Mann-Whitney — En estadística la prueba U de Mann Whitney (también llamada de Mann Whitney Wilcoxon, prueba de suma de rangos Wilcoxon, o prueba de Wilcoxon Mann Whitney) es una prueba no paramétrica aplicada a dos muestras independientes. Es, de hecho, la… …   Wikipedia Español

  • Martin Kruskal — Martin David Kruskal (29 de septiembre de 1925 26 de diciembre de 2006) fue un matemático y físico de Estados Unidos. Contenido 1 Estudios y logros 2 Familia Kruskal 3 Referencias …   Wikipedia Español

  • Joseph Kruskal — Joseph B. Kruskal (29 de enero de 1928 – Maplewood, Nueva Jersey, 19 de septiembre de 2010)[1] fue un matemático y estadístico estadounidense. Contenido 1 Biografía 2 …   Wikipedia Español

  • Estadística no paramétrica — Saltar a navegación, búsqueda La estadística no paramétrica es una rama de la estadística que estudia las pruebas y modelos estadísticos cuya distribución subyacente no se ajusta a los llamados criterios paramétricos. Su distribución no puede ser …   Wikipedia Español

  • Ranking — El texto que sigue es una traducción defectuosa o incompleta. Si quieres colaborar con Wikipedia, busca el artículo original y mejora o finaliza esta traducción. Puedes dar aviso al autor principal del artículo pegando el siguiente código en su… …   Wikipedia Español

  • Escalas Likert — Saltar a navegación, búsqueda La escala de tipo Likert es una escala psicométrica comúnmente utilizada en cuestionarios, y es la escala de uso más amplio en encuestas para la investigación. Cuando respondemos a un elemento de un cuestionario… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”