- Recta polar
-
Recta polar
Para hablar de recta polar es necesario primero hablar de puntos conjugados.
Puntos Conjugados
Sea I una circunferencia. Se dice que un punto C es conjugado de un punto A respecto de la circunferencia I si la circunferencia de diámetro AC es ortogonal a la circunferencia I.
La relación de conjugación es recíproca, el punto A es conjugado del punto C respecto de I y se dice que A y C son puntos conjugados respecto de la circunferencia I.
Recta Polar
La recta polar de un punto A respecto a una circunferencia I es el lugar geométrico de los puntos conjugados de A respecto de la circunferencia I.
Este lugar geométrico resulta ser una recta perpendicular a la recta que une el centro de la circunferencia I con el punto A.
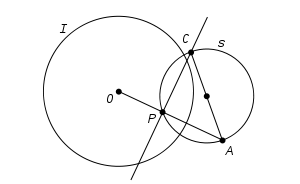
En efecto, sea O el centro de la circunferencia I (véase la figura). Sean A y C puntos conjugados respecto de I y s la circunferencia (ortogonal a I) de diámetro AC. Consideremos la recta OA y sea P la otra intersección de la recta OA con la circunferencia s. Observamos que por estar P sobre la circunferencia s y por ser AC diámetro de dicha circunferencia, el triángulo APC es recto en P. Así, el punto C, conjugado de A respecto de I se halla sobre la perpendicular a la recta OA por el punto P. Como esto vale para todo punto conjugado de A concluimos que dicha recta está contenida en el conjunto de puntos conjugados de A respecto de I.
El recíproco también es cierto: Si C es un punto sobre la perpendicular a la recta OA por el punto P entonces dicho punto es conjugado de A respecto de la circunferencia I.
Esto concluye lo que se quería mostrar.
- Para hallar la recta polar del punto A respecto de la circunferencia I, observemos que la circunferencia s es invariante en la inversión respecto de la circunferencia I. El punto P es por tanto el inverso simétrico de A en esta transformación.
- Se dice que el punto A es polo de la recta PC.
Categoría: Geometría
Wikimedia foundation. 2010.