Una Red de Petri es una representación matemática de un sistema distribuido discreto. Las redes de Petri fueron definidas en los años 1960 por Carl Adam Petri. Son una generalización de la teoría de autómatas que permite expresar eventos concurrentes.

Una red de Petri está formada por lugares, transiciones y arcos dirigidos, así como por fichas que ocupan posiciones. Los arcos conectan un lugar a una transición o una transición a un lugar. No puede haber arcos entre lugares ni entre transiciones. Los lugares contienen un número cualquiera de fichas. Las transiciones se disparan, es decir consumen fichas de una posición de inicio y producen fichas en una posición de llegada. Una transición está habilitada si tiene fichas en todas sus posiciones de entrada.

En su forma más básica, las fichas que circulan en una red de Petri son todas idénticas. Se puede definir una variante de las redes de Petri en las cuales las fichas pueden tener un color (una información que las distingue), un tiempo de activación y una jerarquía en la red.

La mayoría de los problemas sobre redes de Petri son decidibles, tales como el carácter acotado y la cobertura. Para resolverlos se utiliza un árbol de Karp-Miller. Se sabe que el problema de alcance es decidible, al menos en un tiempo exponencial.

Contenido 1 Definición de las Redes de Petri 2 Áreas de aplicación 3 Herramientas de programación 4 Véase también 5 Bibliografía 6 Enlaces externos

Definición de las Redes de Petri

Mediante una red de Petri puede modelizarse un sistema de evolución en paralelo compuesto de varios procesos que cooperan para la realización de un objetivo común.

La presencia de marcas en una ficha se interpreta habitualmente como presencia de recursos. El franqueo de una transición (la acción a ejecutar) se realiza cuando se cumplen unas determinadas precondiciones, indicadas por las marcas en las fichas (hay una cantidad suficiente de recursos), y la transición (ejecución de la acción) genera unas postcondiciones que modifican las marcas de otras fichas (se liberan los recursos) y así se permite el franqueo de transiciones posteriores.

Definición: Una red de Petri es un conjunto formado por R = {P,T,Pre,Post}, dónde P es un conjunto de fichas de cardinal n, T un conjunto de transiciones de cardinal m, Pre la aplicación de incidencia previa que viene definida como

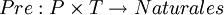
y Post la aplicación de incidencia posterior que viene definida como

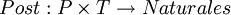
Definición: Una red marcada es el conjunto formado por {R,M} donde R es una Red de Petri como la definida, M es una aplicación denominada marcado y

.

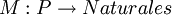Se asocia a cada ficha un número natural, denominado marca. Las marcas para una ficha se reúnen en columnas.

... !!!incompleto!!! (sigue)

Áreas de aplicación

• Análisis de datos
• Diseño de software
• Fiabilidad
• Flujo de trabajo
• Programación concurrente

Herramientas de programación

1. ARP
2. CoopnTools
3. CPN-AMI
4. CPN Tools
5. CPN ML
6. DPNSchematic
7. HiQPN-Tool
8. HPSim
9. Integrated Net Analyzer
10. JARP : Petri Nets Analyzer. Web de desarrollo http://jarp.sourceforge.net/
11. JFern: Rakiura JFern (http://sourceforge.net/projects/jfern) "Java based Petri Net framework (2003)" - framework ligero con simulador, desarrollado en java.
12. JPetriNet: web de desarrollo http://jpetrinet.sourceforge.net/
13. Maria
14. Marigold
15. Model-Checking Kit
16. NEPTUN
17. PED
18. PEP
19. PetriEdiSim
20. Platform Independent Petri Net Editor
21. Petrigen
22. PetriSim
23. Petri Net Browser
24. Petri Net Kernel
25. Petri Net Simulator
26. PNES
27. PNSim
28. PNtalk
29. Poseidon
30. Poses++
31. Predator
32. PROD
33. Renew
34. SEA
35. SimPRES
36. SIPN-Editor
37. SimulaWorks
38. StpnPlay
39. Tina
40. Visual Object Net ++
41. WebSPN
42. WINSIM
43. Woflan
44. Woped
45. XPetri
46. XRL

Véase también

• Autómata finito
• Flujo de trabajo

Bibliografía

• Decidability Issues for Petri Nets a survey. Javier Esparza, Mogens Nielsen 1994
• Harald Störrle: Models of Software Architecture - Design and Analysis with UML and Petri-Nets, Books on Demand GmbH, ISBN 3-8311-1330-0
• Robert-Christoph Riemann: Modelling of Concurrent Systems: Structural and Semantical Methods in the High Level Petri Net Calculus, Herbert Utz Verlag, ISBN 3-89675-629-X
• Kurt Jensen: Coloured Petri Nets, Springer Verlag, ISBN 3-540-62867-3
• Janette Cardoso, Heloisa Camargo: Fuzziness in Petri Nets, Physica-Verlag, ISBN 3-7908-1158-0
• James Lyle Peterson: Petri Net Theory and the Modeling of Systems, Prentice Hall, ISBN 0136619835
• Mengchu Zhou, Frank Dicesare: Petri Net Synthesis for Discrete Event Control of Manufacturing Systems, Kluwer Academic Publishers, ISBN 0792392892
• Mengchu Zhou: Modeling, Simulation, & Control of Flexible Manufacturing Systems: A Petri Net Approach, World Scientific Publishing Company, ISBN 981023029X

Enlaces externos

• YASPER Process Modeling Software
• Petri Nets World
• Petri Net Markup Language
• exchangeable Routing Language
• Citations from CiteSeer
• Introducción a las redes de Petri. Aplicación práctica en multitarea.