- Reducción de conjuntos
-
Reducción de conjuntos
En teoría de la computabilidad, sean A y B dos conjuntos cualesquiera; decimos que A es reducible a B y escribimos A ≤ B, si existe una función computable total, o lo que es el equivalente, una función recursiva primitiva tal que:
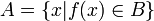
Es decir, f es una función que transforma elementos x ∈ A en elementos y ∈ B y elementos x ∉ A en elementos y ∉ B. O sea:
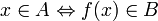
Teoremas relacionados
- Si A ≤ B, entonces:
- Si B es recursivo, entonces A es recursivo.
- Si B es recursivamente enumerable, entonces A es recursivamente enumerable.
Categorías: Computabilidad | Teoría de conjuntos - Si A ≤ B, entonces:
Wikimedia foundation. 2010.
