Conjunto

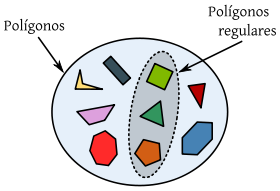Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos —los polígonos regulares en la imagen— es otro conjunto, en particular, un subconjunto del primero.

En matemáticas, un conjunto es una colección de objetos considerada como un objeto en sí. Los objetos de la colección pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Cada uno de los objetos en la colección es un elemento o miembro del conjunto.^[1] Por ejemplo, el conjunto de los colores del arcoíris es:

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}

Un conjunto suele definirse mediante una propiedad que todos sus elementos comparten. Por ejemplo, para los números naturales, si consideramos la propiedad de ser un número primo, el conjunto de los número primos es:

P = {2, 3, 5, 7, 11, 13, ...}

Un conjunto queda definido únicamente por sus miembros y por nada más. En particular el orden en el que se representen estos es irrelevante. Además, cada elemento puede aparecer de manera idéntica una sola vez, esto es, no puede haber elementos totalmente idénticos repetidos. Por ejemplo:

S = {Lunes, Martes, Miércoles, Jueves, Viernes} = {Martes, Viernes, Jueves, Lunes, Miércoles}

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta} = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta, Naranja}

Los conjuntos pueden ser finitos o infinitos. El conjunto de los número naturales es infinito, pero el conjunto de los planetas en el Sistema Solar es finito (tiene ocho elementos). Además, con los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números.

Los conjuntos son un concepto básico, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere pues la introducción de axiomas y conduce a la teoría de conjuntos.

Definición

Georg Cantor, uno de los fundadores de la teoría de conjuntos, dio la siguiente definición de conjunto:^[2]

Los elementos o miembros de un conjunto pueden ser cualquier cosa: números, personas, letras, otros conjuntos, etc. Los conjuntos se denotan habitualmente por letras mayúsculas.

La propiedad más básica de los conjuntos es el hecho de que un conjunto queda definido únicamente por sus elementos.

A y B tienen los mismos elementos si cada elemento de A es elemento de B y cada elemento de B pertenece a A.

Descripción de un conjunto

Conjunto de personas. El conjunto de «personas» mostrado en la imagen, A, tiene 8 miembros. Este conjunto puede representarse mediante llaves o mediante un diagrama de Venn. El orden de las personas en A es irrelevante.

Existen dos maneras de describir o especificar los elementos de un conjunto:

Una de ellas es mediante una definición intensiva, usando una regla o definición semántica:

A es el conjunto cuyos miembros son los cuatro primeros números naturales.

B es el conjunto de colores de la bandera de México.

La segunda manera es por extensión, esto es, listando cada miembro del conjunto. En una definición extensiva se escriben los elementos del conjuntos entre llaves:

C = {4, 2, 3, 1}

D = {blanco, rojo, verde}

Puesto que un conjunto queda especificado únicamente por sus elementos, a menudo pueden usarse ambas definiciones, intensivas y extensivas, para especificar un mismo conjunto. Por ejemplo:

«El conjunto de las vocales en español» = {e, u, a, i, o}

En los ejemplos anteriores, se tiene que A = C y B = D

Debido a la propiedad de la extensionalidad, el orden en el que se especifiquen los elementos de un conjunto es irrelevante (a diferencia de una tupla o una sucesión). Por ejemplo:

C′ = {1, 2, 4, 3} es igual a C = {4, 2, 3, 1}

D′ = {verde, blanco, rojo} es igual a D = {blanco, rojo, verde}

Esto es así debido a que lo único que define un conjunto son sus elementos. Por ejemplo, cada elemento de D es un elemento de D′ y viceversa, luego ambos son necesariamente el mismo conjunto. Del mismo modo, y a diferencia de un multiconjunto, cada elemento de un conjunto es único: no puede repetirse o pertenecer «más de una vez». Esto significa que, por ejemplo:

{4, 3, 2, 4} = {4, 2, 3} ,

ya que los elementos de ambos conjuntos son los mismos: el 4, el 3 y el 2. No sería el caso si los números que consideramos tuvieran alguna otra propiedad que los diferenciase:

{4, 3, 2, 4} es distinto de {4, 2, 3} y de {4, 2, 3}

Es habitual utilizar las llaves también en las definiciones intensivas, especificando la propiedad que define al conjunto:

{Vocales del español} = {o, u, i, e, a}

{Palos de la baraja francesa} = {♠, ♣, ♥, ♦}

Otra notación habitual en matemáticas es:

F = {n² : n es un entero y 1 ≤ n ≤ 10} ,

donde en esta expresión los dos puntos («:») significan «tal que». Así, el conjunto anterior es el conjunto de «los números de la forma n² tal que n es un número natural entre 1 y 10 (ambos inclusive)», o sea, el conjunto de los diez primeros cuadrados de números naturales, {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}. En lugar de los dos puntos se utiliza también la barra vertical («|»).

Relación de pertenencia. El conjunto A es un conjunto de polígonos. En la imagen, algunas de las figuras pertenecen a dicho conjunto, pero otras no.

Pertenencia

La relación clave en un conjunto es la pertenencia: cuándo es un elemento miembro de un conjunto. Si a es un miembro de B, se denota por a ∈ B, y si no lo es, se denota por a ∉ B. Por ejemplo, respecto a los conjuntos A, B y F de la sección anterior, podemos decir:

4 ∈ A , 36 ∈ F , verde ∈ B , pero

7 ∉ A , 8 ∉ F , azul ∉ B

Y se dice entonces que —por ejemplo—, 4 pertenece al conjunto A, es un miembro de A, está en A, etc.

Subconjuntos

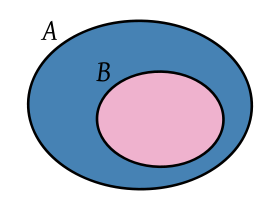Subconjunto. B es un subconjunto de A (en particular un subconjunto propio).

Un subconjunto A de un conjunto B, es un conjunto que contiene algunos de los elementos de B (o quizá todos):

Si A es un subconjunto de B, se escribe como A ⊆ B y se dice que «A está contenido en B». También puede escribirse B ⊇ A, y decirse que B es un superconjunto de A y también «B contiene a A» o «B incluye a A».

Si A no sólo contiene algunos sino todos los elementos B, A no sólo es un subconjunto de B, sino que ambos conjuntos son iguales, A = B. El otro caso posible es que A contenga algunos pero no todos los elementos de B: A es un subconjunto de B pero no son iguales. Se dice entonces que A es un subconjunto propio de B y se denota A ⊊ B, es decir: A ⊆ B pero A ≠ B (y equivalentemente, para un superconjunto propio, B ⊋ A).

(También se utiliza la notación A ⊂ B y B ⊃ A, pero según el autor esto puede denotar subconjunto, A ⊆ B y B ⊇ A; o subconjunto propio, A ⊊ B y B ⊋ A).

Ejemplos.

El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».

{1, 3} ⊊ {1, 2, 3, 4}

{1, 2, 3, 4} ⊆ {1, 2, 3, 4}

Cardinalidad

Los conjuntos pueden ser finitos o infinitos. En el caso de un conjunto finito podemos contar los elementos del conjunto:

El cardinal se denota por |A|, card(A) o #A. Así, en los ejemplos anteriores, se tiene que |A| = 4 (cuatro números), |B| = 3 (tres colores) y |F| = 10 (diez cuadrados). El único conjunto cuyo cardinal es 0 es el conjunto vacío ∅.

En un conjunto infinito no hay un número finito de elementos. Es el caso por ejemplo de los números naturales: N = {1, 2, 3, ...}. Sin embargo, los conjuntos infinitos pueden compararse, y resulta que existen conjuntos infinitos «más grandes» que otros. El «número de elementos» de un conjunto infinito es un número transfinito.

Operaciones con conjuntos

Operaciones con conjuntos

Existen varias operaciones básicas que pueden realizarse para, partiendo de ciertos conjuntos dados, obtener nuevos conjuntos:

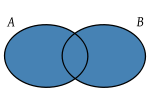
• Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B obtenido al juntar todos los elementos de A y de B.
• Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B de los elementos comunes a A y B.
• Diferencia. La diferencia del conjunto A con B es el conjunto A \ B que resulta de eliminar de A cualquier elemento que esté en B.
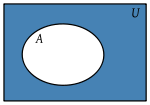
• Complemento. El complemento de un conjunto A es el conjunto A^∁ que contiene todos los elementos que no pertenecen a A.
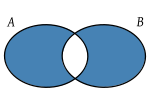
• Diferencia simétrica. La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
• Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B de todos los pares ordenados (a, b) formados con un primer elemento a perteneciente a A, y un segundo elemento b perteneciente a B.

Ejemplos

• {1, a, 0} ∪ {2, b} = {2, b, 1, a, 0}
• {5, z, ♠} ∩ {♠, a} = {♠}
• {5, z, ♠} \ {♠, a} = {5, z}
• {♠, 5} Δ {8, #, ♠} = {5, #, 8}
• {1, a, 0} × {2, b} = {(1, 2), (1, b), (a, 2), (a, b), (0, 2), (0, b)}

Empleo

• En la Topología
• En Probabibilidades, en muestreo.
• En la fundamentación de sistemas numéricos, al construir los números naturales como clases de equivalencia, y en esta perspectiva los enteros, los racionales y los reales como clases de equivalencia de sucesiones de Cauchy.
• En el álgebra moderna: orden parcial e intersección.
• En Análisis matemático para definir los dominios y contradominios de las funciones.

Véase también

Referencias

• Cantor, Georg (2006) [1872-1899]. Fundamentos para una teoría general de conjuntos. Escritos y correspondencia selecta.. Edición de José Ferreirós. Crítica. ISBN 84-8432-695-0. 
• Courant, Richard; Robbins, Herbert; Stewart, Ian (1996) (en inglés). What is Mathematics? An Elementary Approach to Ideas and Methods. Oxford University Press. ISBN 0-19-510519-2.  Suplemento del capítulo II.
• Enderton, Herbert B. (1977). Elements of set theory. Academic Press. 
• Ivorra, Carlos, Lógica y teoría de conjuntos, http://www.uv.es/ivorra/Libros/Logica.pdf, consultado el 18-04-2011 .
• Jech, Thomas. Edward N. Zalta (ed.): «Set Theory» (en inglés). The Stanford Encyclopedia of Philosophy (Spring 2009 Edition). Consultado el 22-04-2011.
• Pla i Carrera, Josep (2003). La verdad matemàtica. publicacions Reial Acadèmia de Doctors. 

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre ConjuntosCommons.
• Weisstein, Eric W., «Set» (en inglés), MathWorld, http://mathworld.wolfram.com/Set.html, consultado el 22-04-2011 

• Este artículo fue creado a partir de la traducción del artículo Set de la Wikipedia en inglés, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.