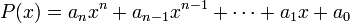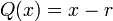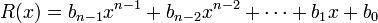En álgebra, la Regla de Ruffini (debida al italiano Paolo Ruffini) nos permite dividir un polinomio entre un binomial de la forma (x − r) (siendo r un número entero). También nos permite localizar raíces de un polinomio y factorizarlo en binomios de la forma (x − r) (siendo r un número entero).

La Regla de Ruffini establece un método para división del polinomio

entre el binomio

para obtener el cociente

y el resto s.

El algoritmo es, de hecho, una división de dos polinomios (P(x) entre Q(x)).

Algoritmo general

Para dividir P(x) entre Q(x):

1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de P(x) y los escribimos ordenados. Entonces escribimos r en la parte inferior izquierda del eje, encima de la línea:

    |        an        an-1       ...        a1         a0
    |                                    
 r  |                                    
----|---------------------------------------------------------
    |                                    
    |                                    

2. Pasamos el coeficiente más pegado a la izquierda (a_n), abajo, justo debajo de la línea para obtener el primero de los coeficientes b:

    |        an        an-1       ...        a1         a0
    |                                    
  r |                                    
----|---------------------------------------------------------
    |        an                     
    |
    |  = bn-1                                
    |

3. Multiplicamos el número más pegado a la derecha debajo de la línea, por r y lo escribimos sobre la línea en la primera posición de la derecha:

    |        an        an-1       ...        a1         a0
    |
  r |                  bn-1r
----|---------------------------------------------------------
    |        an
    |
    |      = bn-1                                
    |

4. Añadimos los dos valores que hemos puesto en la misma columna:

    |        an        an-1       ...        a1         a0
    |
  r |                  bn-1r
----|---------------------------------------------------------
    |        an     an-1+(bn-1r)
    |
    |      = bn-1     = bn-2                                
    |

5. Repetimos los pasos 3 y 4 hasta que no tengamos más números:

    |        an        an-1       ...        a1         a0
    |
  r |                  bn-1r      ...        b1r        b0r
----|---------------------------------------------------------
    |        an     an-1+(bn-1r)  ...       a1+b1r       a0+b0r
    |
    |      = bn-1     = bn-9      ...       = b0        = s
    |

Los valores b son los coeficientes del polinomio resultante (R(x)), el grado será menor que el grado de P(x). s será el resto (viloni).

También en la regla de Ruffini el divisor se multiplica por todos los números.Se ponen los números y se va poniendo el resultado.El resto siempre es el último número.

Véase también

• polinomio
• operaciones con polinomios
• Raíz de la unidad