La regla de cálculo es un instrumento manual de cálculo que dispone de varias escalas numéricas, para facilitar la rápida y cómoda realización de operaciones aritméticas complejas, como puedan ser multiplicaciones, divisiones, etc. A cambio de ello, no ofrece más que una precisión limitada. Su época de esplendor duró más de un siglo, el periodo comprendido entre la segunda mitad del siglo XIX y el último cuarto del XX, aunque había sido inventada mucho antes. La regla de cálculo fue sustituida paulatinamente por las calculadoras y los ordenadores electrónicos conforme fueron avanzando los últimos decenios del siglo XX.

Contenido 1 Historia 2 Características principales 2.1 La regla 2.2 El círculo de cálculo 2.3 Precisión 2.4 Formas y materiales 3 Manejo de la regla cálculo 4 Escalas y tipología 4.1 Tipos básicos 4.2 Escalas habituales 5 Fundamento teórico 5.1 Nomogramas estáticos 5.2 Escalas móviles 5.2.1 Suma de segmentos 5.2.2 Multiplicación 6 Bibliografía 7 Enlaces externos

Historia

Los inicios de la regla de cálculo son bastante confusos. Todavía a principios del siglo XX había tres o cuatro candidatos al título de inventor de la misma. Tras muchas controversias, la opinión de los historiadores es que fue inventada en el periodo 1620-1630, pocos años después del descubrimiento por John Napier del concepto y propiedades de los logaritmos naturales en 1614, y una vez que se realizó su conversión a la base decimal por Henry Briggs en 1617.

Edmund Gunter fue el primero que expuso los logaritmos en una escala lineal. Esta era la famosa línea de Gunter, dada a conocer en su libro Canon triangulorum, que publicó en Londres en 1620. Y hacia 1621 William Oughtred –el gran matemático inglés de la época y amigo de Napier, al igual que lo eran Briggs y Gunter–, yuxtapuso las escalas de dos líneas de Gunter, ideando así la regla de cálculo actual, tanto en su versión lineal como circular. Pero Oughtred era un profesor de matemáticas riguroso, que pretendía que sus alumnos aprendiesen a razonar y conociesen a fondo la disciplina, no que se distrajeran con la utilización de artilugios mecánicos, de modo que durante mucho tiempo reservó el ingenio para su propio uso, sin darle publicidad.

Pero uno de sus discípulos, Richard Delamain, tuvo conocimiento del hecho y fue el primero en publicar información relativa a una regla circular hacia 1630, atribuyéndose el invento, de lo que derivaron enconadas disputas sobre su prioridad con Oughtred, quien pasó a otro de sus alumnos, William Forster, sus notas sobre el particular, escritas en latín, para que las diese a conocer. Forster las tradujo al inglés y en 1632 apareció la obra titulada The circles of proportion and the horizontal instrument, incluyendo al final de la misma una Apologeticall epistle en la que Oughtred respondía a los ataques de Delamain, al tiempo que le criticaba.

Todos estos instrumentos matemáticos se utilizaron preferentemente en tareas prácticas de cubicaje y aforo de mercancías, tanto por los comerciantes en maderas, cereales, vino, aceite, etc., como por los funcionarios de aduanas y fielatos encargados de cobrar cánones por ellas. También encontraron aplicación en la navegación marítima, aunque casi exclusivamente en Inglaterra, donde no sólo se realizaron las invenciones más importantes con ellas relacionadas, sino que además existían bastantes artesanos capaces de fabricar instrumentos de cierta precisión (como los Allen, los Brown o Henry Sutton), que trabajaban en estrecho contacto con los inventores y realizaban los prototipos y las sucesivas copias.

Las peculiaridades del sistema de medidas inglés puede que tuviesen bastante que ver en esta falta de difusión. Hay que esperar a los principios del siglo XIX para que la regla de cálculo empiece a ser ampliamente conocida en Francia, y luego en Alemania, y a los comienzos del XX para que se convirtiese en instrumento de uso profesional y estudiantil muy generalizado.

En lo que a la concepción de los aparatos se refiere, la actividad creadora fue incesante en los tres siglos y medio de vigencia que tuvieron. Muchas de las ideas y propuestas no pasaron de la teoría o de la construcción de un prototipo, pero hubo algunas que lograron una cierta implantación. Las primeras reglas de composición integrada, similares a las actuales, fueron fabricadas por Seth Partridge en 1658.

La idea del hilo como parte integrante de estos instrumentos nomográficos, probablemente fue expresada por primera vez por Newton en 1675, aunque el cursor como tal fue desarrollado por John Robertson en 1775. Thomas Everard incorporó una escala inversa en 1683. Su regla tuvo bastante difusión, como también la tuvo otro modelo para carpintería desarrollado por Henry Coggeshall en 1677. Ambos instrumentos eran de madera, pero bastante toscos y poco precisos.

Hacia 1779 James Watt y Mathew Boulton modificaron, para sus propios trabajos con la máquina de vapor, reglas de cálculo fabricadas por John Rowley, mejorando la división de las escalas y la precisión del aparato, que terminó siendo conocido como tipo Soho, por el nombre de su factoría de Birmingham. Esto difundió el uso del instrumento entre los ingenieros mecánicos.

La idea de las escalas doblemente logarítmicas (que permiten realizar operaciones de potenciación y de extracción de raíces con cualquier exponente, positivo o negativo, de una sola vez) la propuso inicialmente Peter Mark Roget en 1815, pero cayó en el olvido, para ser luego reinventada varias veces, al menos, por J. H. Thomson en 1881, por John Perry en 1901 y por Hubert Boardman en 1933. Su incorporación a las reglas comerciales no se produjo hasta bien avanzado el siglo XX.

La utilización de las dos caras de la regleta para la realización de cálculos (sistema dúplex) fue patentada por William Cox en 1891, siendo fabricada por la empresa norteamericana Keuffel and Esser.

Las reglas de cálculo cayeron en desuso con la popularización de la calculadora electrónica. En ingeniería, sucedió fundamentalmente con la aparición en el mercado del modelo HP-35 de Hewlett-Packard en 1972. Hacia 1980 había cesado prácticamente la producción de reglas de cálculo, aunque todavía siguen fabricándose instrumentos de este tipo en pequeñas cantidades para usos muy específicos en sectores industriales, de navegación marítima y aérea o para atender a un minoritario mercado de aficionados y coleccionistas.

Características principales

La regla

La regla de cálculo consta de varias partes, como puede apreciarse en la imagen, perteneciente a un modelo estudiantil corriente de finales del siglo XX.

Hay en primer lugar, un soporte básico o cuerpo, generalmente paralelepipédico, que tiene una ranura longitudinal profunda en su parte central, lo que determina la aparición de dos sub-unidades, a saber, una regleta superior y otra inferior, más estrechas. En algunos modelos, como en el reproducido a la derecha, se trata efectivamente de dos piezas independientes, vinculadas entre sí rígidamente por abrazaderas situadas en sus extremos. Por la ranura central se desliza otra pieza en forma de regleta de menor tamaño, también llamada corredera.

En las caras frontales de estas piezas es donde están grabadas las diversas escalas. A veces la regleta móvil también ofrece escalas en su parte trasera, para cuyo uso se la ha de insertar a la inversa en el soporte básico o bien pueden leerse sus datos a través de orificios practicados en la superficie posterior del cuerpo. La parte trasera de éste también se aprovecha eventualmente para inscribir datos numéricos de interés o incluso otro conjunto completo de escalas; a los modelos así ampliados se les suele llamar dúplex, frente a la denominación de simplex aplicada a los que no son operativos más que por su cara frontal. El cuerpo de los modelos dúplex es necesariamente de dos piezas ensambladas. Han existido a lo largo de la historia algunos aparatos con varias regletas móviles.

Por último suele haber una pieza móvil y transparente, que abarca la totalidad de la superficie frontal (o del anverso y el reverso en el caso de las dúplex), y que no lleva grabada más que una fina línea de referencia, llamada hilo, índice o retículo, aunque a veces puede que haya alguna otra línea auxiliar. A esta pieza se le llama cursor y sirve para facilitar la alineación y la lectura de los factores que intervienen en las operaciones, sobre todo cuando las escalas intervinientes están alejadas entre sí; en los modelos dúplex resulta esencial para transferir datos de una cara a otra del aparato. Los cursores de algunas reglas actúan como una lupa para mejorar el detalle de las lecturas. A partir del segundo cuarto del siglo XX se realizaron algunos cursores de mayor complicación mecánica: pivotados radialmente, articulados, etc., pero nunca fueron muy populares, habiendo sido concebidos para usos muy especiales.__

El círculo de cálculo

Denominado habitualmente "regla de cálculo circular", es la única forma del instrumento que merece una mención específica aparte de la regla, no sólo porque fue inventada desde los inicios sino por ofrecer algunas características muy ventajosas. Por lo pronto, para una misma longitud de las escalas tiene una forma más compacta que la regla. Mecánicamente es más sólida y pudiera ser más exacta, al no depender el movimiento más que del eje central. Además, el resultado de las operaciones no "se sale" nunca de la escala, que normalmente es una curva cerrada, aunque también las hubo en forma de espiral. A cambio de ello, es de uso un poco menos intuitivo, ya que la precisión disminuye en las escalas que ocupan posiciones más interiores en el círculo y la interpolación visual parece resultar algo más difícil que en la regla. Nunca ha gozado de la popularidad de ésta; muchas veces se usaron como vehículo de promociones publicitarias.

Se han fabricado en dos estilos básicos diferentes. Uno de ellos consiste en un par de círculos concéntricos con un cursor radial, fijo o móvil. Los círculos deben estar encastrados para un adecuado funcionamiento; de otro modo el aumento de la paralaje introduce errores en los cálculos. Otro consta de un disco fijo, con dos cursores móviles independientes, pero que pueden solidarizarse. Quizá haya que considerar como pertenecientes a un tercer tipo a los modelos que adoptan la forma de relojes de bolsillo, y hasta de pulsera, manejándose el movimiento de los círculos y de los cursores mediante coronas exteriores; su prototipo fue concebido por A. E. M. Boucher en 1876.

Precisión

Lo esencial del instrumento son las escalas numéricas, unas fijas y otras móviles, mediante las que se realizan las operaciones. La precisión que pueda conseguirse de un aparato determinado depende de la longitud que en él tengan estas escalas, pues viene limitada por las estimaciones de valores que pueda realizar quien lo utilice, proceso consustancial al método y al que se denomina interpolación visual o a la vista. Se han construido reglas de muy diversos tamaños, lo que en principio podría parecer arbitrario, pero no lo es; si el trabajo a realizar es delicado, deberá utilizarse la regla más larga posible. Por ejemplo, para conseguir una precisión de una parte en 10.000 la escala ha de tener una longitud de 12 m (como sucede en el modelo cilíndrico de Fuller, fabricado a partir de 1878). Los tamaños habituales no superan las tres cifras significativas en manos experimentadas, pues la última ya será casi siempre estimada.

Naturalmente lo anterior presupone que las marcas de las escalas están hechas con absoluta precisión sobre las reglas. Esto es una suposición razonable en los ejemplares actuales, en concreto en los comercialmente disponibles a partir de comienzos del siglo XX, en que empezaron a aplicarse técnicas mecánicas precisas de fabricación, pero no lo es en absoluto para los precedentes, cuyas escalas estaban realizadas individualmente o con técnicas deficientes, por lo que muchos de ellos resultaban bastante alejados de la perfección. Esta fue otra razón importante para la lentitud con que se extendió su uso.

Se ha manifestado la opinión que la limitada precisión de la regla de cálculo es una ventaja y no un inconveniente cuando se trata de aplicaciones prácticas, pues los datos disponibles sobre los que versa el cálculo no suelen superar las tres cifras significativas. Se evita así con ella el espejismo de la falsa precisión, al que pueden inducir las calculadoras electrónicas si no se utilizan prudentemente.

Formas y materiales

A lo largo de los tiempos estas escalas han variado mucho en naturaleza, tamaño y número y se han organizado de muy variadas formas, disponiéndoselas sobre superficies rectangulares, circulares y cilíndricas. La realización más común es la que utiliza una tablilla rectangular plana, de la que deriva su nombre de "regla". Los materiales utilizados han dependido de las épocas, lugares y técnicas de construcción disponibles. Se han fabricado de cartón y papel maché, de maderas duras (como el boj), de bambú, metálicas (de bronce, latón y otros metales), de diversos materiales plásticos, etc.

Manejo de la regla cálculo

Lo fundamental para poder utilizar bien la regla de cálculo es comprender la naturaleza de sus escalas. En el caso de las básicas esto no ofrece mayor dificultad, como tampoco lo hace en el caso de las más usuales, sobre todo si están rotuladas con los símbolos antes indicados en la tabla.

De no ser así se necesita consultar el manual del modelo concreto de regla de que se disponga (lo que no suele ser fácil porque es lo primero que se pierde del conjunto). Afortunadamente ahora se dispone de bastante información al respecto en la red, con la que quizá pueda suplirse esta deficiencia. Por ejemplo, puede resultar útil consultar el manual del modelo Faber-Castell Novo-Biplex 2/83 N , que es bastante detallado y trata de una regla que disponía de muchas escalas. Los manuales en español de muchos modelos europeos, entre ellos el acabado de referir, junto con otra amplia información, pueden obtenerse aquí.

Las otras dos habilidades fundamentales con que se ha de contar son: la práctica en la lectura de los valores y la fijación del punto decimal.

Las superficies de las reglas de cálculo suelen estar muy congestionadas, en un intento de dotarlas de la máxima funcionalidad, por lo que es fácil confundirse tanto al establecer los valores iniciales como al obtener el resultado. Además de ello hay que estimar sus últimas cifras. Los remedios aplicables para sortear estos peligros son: a) poner la atención necesaria al operar y b) contar con un poco de práctica.

Las escalas logarítmicas no indican más que la parte decimal de los números, la llamada mantisa. En el caso de los logaritmos decimales la parte entera, llamada característica, es el exponente de la potencia de diez correspondiente al dato. El logaritmo de 5600 es 3,74819 (= exp 10³ + 0,74819) y el de 5,6 es 0,74819 (= exp 10⁰ + 0,74819). Por eso la escala se repite cada diez enteros, en lo que se llama a veces un ciclo. Las escalas C y D, las escalas básicas de toda regla de cálculo, son escalas de un ciclo, no abarcan más que de 1 a 10, pero este último 10 también se representa mediante un 1 por ser el comienzo de la siguiente decena. Las escalas A y B son escalas de dos ciclos, dispuestos en el mismo espacio que la decena de las C y D. Por eso sus valores representan los cuadrados de éstas y así sucesivamente. Pero eso quiere decir que hay que tener cuidado de no confundir la primera decena con la segunda, ni las primeras cifras de los números con las segundas. Por ejemplo, 1,5² es 2,25, pero las marcas que para ello han de alinearse en las diversas escalas son: una que ostenta encima un 5 y otra sin cifra, comprendida entre el 2 y el 3, a la que hay que asignarle el valor. Para actuar con seguridad es imprescindible contar con el auxilio de una operación mental aproximada. Si se calculan mentalmente los cuadrados de 1 y de 2, se tendrá el convencimiento que 2,25 es un valor razonable para el cuadrado de 1,5 y que por tanto la operación se ha hecho bien. Si lo que se calcula en cambio es 4,2² es evidente que la respuesta no puede ser 1,76, que es lo que literalmente indica la escala, sino que ha de ser superior a 10, e incluso a 16, y por tanto es 17,6. Hay que tener el sentido de la serie de potencias de 10; y, si no se tiene, hay que adquirirlo.

Si la solución del problema en el que se esté utilizando la regla de cálculo implica una serie de operaciones encadenadas, lo más seguro es anotar los resultados intermedios en un papel con un lápiz. Con algo de práctica puede utilizarse también el cursor para estas transferencias en bastantes casos.

La naturaleza exhaustiva de las soluciones nomográficas hace que, si un nomograma puede realizar determinada operación aritmética, también pueda realizar su inversa. Por tanto, cuando se habla de elevación a potencias se está hablando simultáneamente de extracción de raíces de esos mismos exponentes, cuando de multiplicación, también de división, etc. Lo único que se requiere para pasar de una a otra es aplicar el mismo procedimiento cambiando el orden de las escalas.

Escalas y tipología

Durante los dos primeros siglos de su existencia las reglas de cálculo fueron productos artesanos, fabricados individualmente y en cantidades muy menguadas, cuando no únicos. Las funciones para las que se las preparaba eran pues las solicitadas por el inventor o el cliente (que muchas veces coincidían en la misma persona) o las que acostumbrase a realizar el artesano correspondiente.

Conforme avanzaba el siglo XIX y aumentaban los conocimientos científicos y técnicos, así como la industrialización, el tipo de cálculos realizados por un creciente número de ingenieros civiles y militares creó un mercado propicio para la difusión de este instrumento. Surgieron así pautas estables en el número y naturaleza de las escalas incluidas en las reglas que se ofrecían comercialmente.

Tipos básicos

La primera de ellas se debió a un artillero francés, Amédée Mannheim, quien proyectó en 1850 la primera regla de cálculo que se hizo verdaderamente popular. Parte de este éxito se debió a la inclusión en su modelo del cursor, del que carecía la mayoría de las reglas precedentes, lo que realizó en 1851. Este modelo fue adoptado por el ejército francés y empezó a fabricarse industrialmente a partir de 1859.

Las escalas normalmente vienen identificadas sobre el cuerpo de la regla por un símbolo alfabético grabado en su extremo izquierdo. Sin que sea absolutamente uniforme, esta terminología está bastante aceptada por los diversos fabricantes y la siguiente tabla detalla las designaciones y funciones más extendidas de las escalas más habituales. En algunos casos se especifica también la función matemática correspondiente, lo que suele hacerse en el extremo derecho de la escala.

Lo mismo sucede con los tipos genéricos de regla. Aunque casi todos los modelos tengan escalas adicionales, los tres tipos básicos y las escalas que implican son:

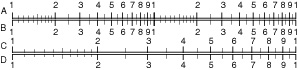
• Mannheim: A, B, C, D.
• Rietz; A, B, C, D, K, L, S, T, ST, CI (pauta propuesta por Max Rietz en 1902).
• Darmstadt: añade fundamentalmente las escalas LL al modelo Rietz (pauta propuesta por Alwin Walther en 1934).

Escalas habituales

Designación	Descripción	Valor
A	escala de cuadrados; escala logarítmica de dos decenas, situada en el borde inferior de la regleta fija superior	x²
B	escala de cuadrados, escala logarítmica de dos decenas, situada en el borde superior de la regleta móvil	x²
C	duplicado de la escala básica; escala logarítmica de una decena, situada en el borde inferior de la regleta móvil	x
D	escala básica; escala logarítmica de una decena, situada en el borde superior de la regleta fija inferior	x
K	escala de cubos; escala logarítmica de tres decenas	x³
CI	escala C "invertida", numerada de derecha a izquierda; escala de recíprocos	1/x
CF	escala C "desplazada"; su origen es un valor constante distinto de la unidad, generalmente pi o algún submúltiplo suyo	(pi) * x
S	escala de ángulos de senos	sen-1 x
T	escala de ángulos de tangentes	cos-1 x
ST	escala de senos y tangentes de ángulos pequeños (0,58º a 5,73º); conversiones grado-radian	arc x
L	escala lineal usada para obtener las mantisas de los logaritmos comunes o decimales (base 10)	log x
Ln	escala lineal utilizada para la obtención de los logaritmos naturales (base e)	ln x
LLn	conjunto de escalas doblemente logarítmicas (log-log), utilizadas para las operaciones con exponentes. Pueden tener cualquier base (aunque usualmente sea el número e) y son absolutas (no requieren estimación de la posición del punto decimal).	nx

Las reglas especializadas utilizan muchas otras escalas, adecuadas a los cálculos a que se destinan (p. ej. estadísticos o de ingeniería eléctrica), prescindiendo a veces de algunas de las anteriores.

Muchas reglas de cálculo escolares incluyen además una escala ordinaria de longitud, graduada en cm, en uno de sus bordes.

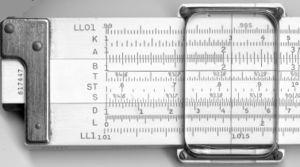
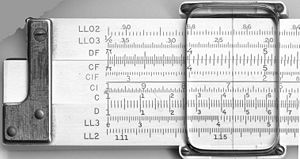
Escalas de las caras anterior y posterior de una regla dúplex K&E 4081-3.

Fundamento teórico

Conviene agrupar en dos categorías distintas las operaciones matemáticas que pueden realizarse con la regla de cálculo.

Nomogramas estáticos

En una de ellas las escalas funcionan como las de un nomograma sencillo, permaneciendo fijas, y lo único que ha de moverse para obtener los resultados es el cursor o el hilo, aunque en muchos casos también podrían conseguirse sin él. Es lo que sucede, por ejemplo, en una regla que disponga de la escala D en la regleta inferior y de la A en la superior (es decir, prácticamente en cualquiera). Las operaciones de elevar al cuadrado y de obtener la raíz cuadrada de un número no requieren para nada de la regleta móvil y a veces ni siquiera del cursor, pudiendo realizarse a ojo muchas de ellas. Estas operaciones vienen representadas por ecuaciones de dos variables, y = f(x), donde la función puede ser la exponenciación, alguna de las trigonométricas, la obtención de logaritmos, etc.

Escalas móviles

Las operaciones de la segunda categoría requieren que se realicen movimientos de la regleta intermedia. D'Ocagne llamaba instrumentos nomo-mecánicos a los que utilizan algún recurso mecánico sencillo para producir las coincidencias geométricas requeridas por el uso de un nomograma. Esto es lo que sucede en el presente caso.

Tales operaciones se reducen a dos, a saber, la suma y la multiplicación (con sus inversas la resta y la división). Tal exigencia adicional deriva de que son las únicas ecuaciones de tres variables, z = f(x, y), que suelen resolverese con la regla de cálculo. En estos casos lo que se realiza sustancialmente es una suma (o resta) de segmentos lineales.

Suma de segmentos

Suele decirse que la regla de cálculo no sirve para sumar, lo que en alguna medida es cierto, pero no contradice la afirmación precedente. Para convencerse de ello basta con deslizar las escalas de dos reglas ordinarias una sobre otra. Si, por ejemplo, la marca inicial de la escala superior se sitúa frente al número 3 de la inferior, se comprobará que ahora cada uno de los demás números de la escala superior se encuentra frente a otro de la inferior que es igual a la suma de él mismo y de 3.

Si la regla de cálculo ordinaria no tiene escalas para realizar sumas no es pues por una incapacidad consustancial, sino por las dos siguientes razones: 1) la suma es una operación que todo el mundo está educado para realizar mentalmente, y casi de modo inconsciente, cuando no tiene más que dos factores y éstos no son excesivamente grandes; y 2) si se incluyesen escalas para la suma en la regla de cálculo, la longitud de ésta tendría que ser muy inconveniente para que el hecho resultase de alguna utilidad. Por ejemplo, una regla de cálculo de 25 cm de largo no podría realizar sumas mayores de "16+9" ("160+90" si se acudiese a las marcas de mm), para lo cual nadie suele necesitar ayuda mecánica alguna. (Para contrarrestar esta limitación el fabricante europeo Faber-Castell adosó a la parte trasera de alguno de sus modelos una sencilla máquina de sumar digital y mecánica de seis cifras, llamada Addiator, durante un periodo comprendido entre 1950 y 1970 aproximadamente.)

Multiplicación

Lo que hay que explicar es más bien lo contrario. Es decir, si la regla de cálculo deslizante lo que fundamentalmente hace son sumas, ¿cómo puede utilizarse para multiplicar y dividir? Parece que tuviese que haber algún truco escondido. Y en efecto lo hay; se trata de un truco nomográfico, que consiste en calibrar de otra manera las escalas utilizadas. Para comprenderlo bien, sigamos paso a paso este proceso de calibración, para lo que conviene volver a la escala habitual de una regla ordinaria, graduada en cm.

Situemos bajo ella otra línea, que marcaremos según los valores de los logaritmos decimales de los números de la primera escala. Esta segunda escala tiene su origen, su punto 0, coincidente con el de la primera, situándose sus restantes marcas a la altura que les corresponde en la primera según los valores de los logaritmos sucesivos, algunos de los cuales aparecen escritos en la siguiente línea, rotulada "log", a la izquierda de la figura inferior. Y para mayor claridad todavía pude colocarse debajo el guarismo correspondiente, línea que se etiqueta como "x" en esta figura. Se trata, en suma, de la representación gráfica de la ecuación y = log x. La primera línea de cifras representa los valores de y y la segunda los de x.

Como lo que aquí interesa no es el valor absoluto de las cifras de y, sino el espaciamiento relativo de los valores, puede despejarse el panorama suprimiendo la primera indicación y dejando solo visibles los valores de la variable independiente, x, así:

Esto fue lo que hizo Edmund Gunter en 1620, inscribiendo una parecida en un instrumento matemático en forma de regla, de más de medio metro de longitud, que contenía también otras varias escalas útiles para la práctica mercantil y marinera. Los cálculos se realizaban aplicando sobre ellas las magnitudes de los factores por medio de compases, modo de proceder hoy casi inimaginable, pero que era muy habitual en la época.

Si el proceso de suma de segmentos se repite ahora utilizando dos de estas escalas, el resultado es muy distinto del que se obtuvo anteriormente:

La escala superior se ha desplazado 1,5 unidades sobre la inferior, pero la cifra que se obtiene debajo de cada marca superior no es ahora la del número correspondiente sumado a 1,5, sino la de dicho número multiplicado por 1,5. El milagro está realizado. Probablemente convenga más decir la magia, que consta de dos partes. Por un lado la calibración logarítmica transmuta la suma de segmentos en multiplicación, por la propiedad de los logaritmos que se formula: log a + log b = log (a x b). Por otro el rotulado final de la escala le da la apariencia de que se refiere directamente a los números; los logaritmos desaparecen de la escena y todo retorna a su aspecto aritmético inicial.

Bibliografía

• Cajori, F.: A history of the logarithmic slide rule and allied instruments (1910) y On the history of Gunter's scale and the slide rule during the seventeenth century (1920). Reunidos en un volumen por Astragal Press. Mendham, N. J., 1994. ISBN 1-879335-52-2.
• Versión electrónica de la primera de las obras precedentes, History of the logarithmic slide rule, en formato PDF.
• D'Ocagne, M.: Le calcul simplifié par les procédés mécaniques et graphiques. Gauthier-Villars. París. 1ª edición, 1894 (¿?); 2ª ed. ampliada, 1905; 3ª ed. completamente revisada y ampliada, 1928. Traducción inglesa de esta última por J. Howlett y M. R. Williams, con introducción y notas: Le calcul simplifié: graphical and mechanical methods for simplifying calculation. Volumen 11 de la "Charles Babbage Institute Reprint Series for the History of Computing". The MIT Press y Tomash Publishers. 1986. ISBN 0-262-15032-8.
• Hopp, P. M.: Slide rules. Their history, models and makers. Astragal Press. Mendham, N. J., 1999. ISBN 1-879335-86-7.
• Turner, A.: artículo Draughting devices en Glazebrook, R. (ed.): Dictionary of applied physics, vol. III: 273. Macmillan and Co. London, 1923.
• Von Jezierski, D.: Slide Rules: A Journey Through Three Centuries. Astragal Press. Mendham, N. J. ISBN 1-879335-94-8.

Enlaces externos

Historia

• The history, theory and use of the engineering slide rule por James B. Calvert, de la Universidad de Denver.
• Oughtred Society Slide Rule Home Page. Asociación dedicada a la historia y la conservación de las reglas de cálculo.
• Early calculators: Slide rules. Museum of HP Calculators.

Información general

• Información general y manuales, en español.
• How a slide rule works. Slide Rule Universe.
• Clark McCoy, información histórica, información sobre los modelos K&E: catálogos, y manuales digitalizados.

Reglas de cálculo virtuales

• Derek's Virtual Slide Rule Gallery. Siete modelos virtuales con ejemplos de uso.
• Sag Milling's Online Sliderule. Regla virtual operativa.

Hágalo usted mismo

• How to make your own slide rule, de Sphere Research.
• Make your own circular slide rule, por Charles Kankelborg, Department of Physics, Montana State University.